33
What is the fastest FizzBuzz?
I watched a video by Nick White, in which he gave strangers $100 if they could solve simple coding videos, one of which being FizzBuzz.
Whenever I see FizzBuzz, I always want to know what the absolute fastest one is. Normally people optimize the printing, or calculating sequential FizzBuzzes, but what's the fastest way to find which word to print for an arbitrary number?
For my tests I decide each function should return a number based on the fizzbuzzality, since actually printing to the console is slow. 0 means the number itself should be printed, 1 means Fizz, 2 means Buzz, and 3 means FizzBuzz.
To test this I set up a bunch of different ways to do it in QuickBench, with an incrementing counter inside the benchmark loop to prevent the function from being optimized away.
I compile using Clang 11.0.0 with the args
I compile using Clang 11.0.0 with the args
-std=++2a -O3.First let's try a simple FizzBuzz implementation:
if(n % 15 == 0){
return 3;
}
if(n % 3 == 0){
return 1;
}
if(n % 5 == 0){
return 2;
}
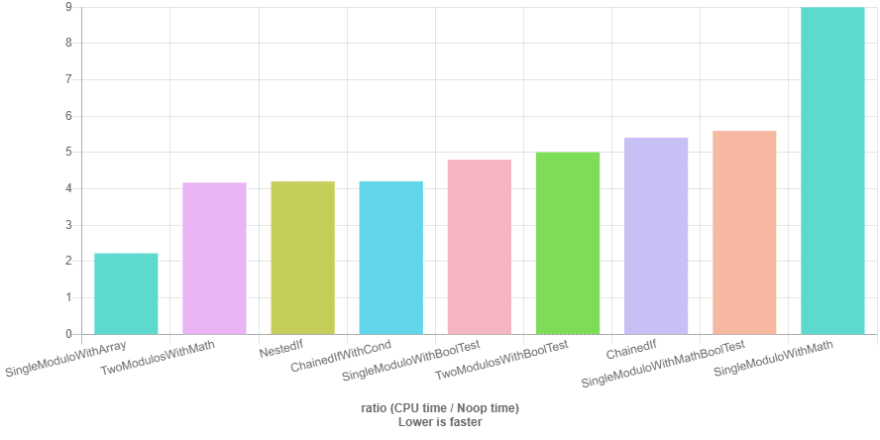
return 0;Running this on QuickBench gives us ~5.41 cpu_time, most of it probably coming from the three modulos / if tests. Branching is notoriously slow, but a good compiler should be able to replace if tests with a conditional operator instead.
That said, we can have almost the same code with only two modulos / if tests instead:
int v = 0;
if(n % 3 == 0){
v += 1;
}
if(n % 5 == 0){
v += 2;
}
return v;This runs at only ~4.21 cpu_time, clearly taking use of conditional add operations. It sometimes has a magic side effect of speeding up the previous func, but I failed to reproduce this later.
Apropos only two modulos, there's another simple FizzBuzz implementation:
if(n % 3 == 0){
if(n % 5 == 0){
return 3;
}
return 1;
}
if(n % 5 == 0){
return 2;
}
return 0;This uses a nested if statement, but only runs at ~4.20 cpu_time, meaning the compiler manages to optimize it quite well.
However, there are more ways of getting only two modulo operations. For example:
bool a = (n % 3) == 0;
bool b = (n % 5) == 0;
if(a&&b) return 3;
if(b) return 2;
if(a) return 1;
return 0;This however runs at ~5.00 cpu_time, only slightly faster than the first function using chained ifs. I imagine there's some branches that aren't properly getting optimized here.
But we can do better!
bool a = (n % 3) == 0;
bool b = (n % 5) == 0;
return b*2+a;This runs at only ~4.17 cpu_time, the fastest so far! This only works if false is 0, and true is 1, so if == ever works differently then it's in big trouble.
Because the second operand of our modulo operation is always known compile-time, having less modulo operators doesn't necesarilly give that much of a speed boost. That said, we want all speed boosts we can get, so:
int a = n%15;
if(a==0) return 3;
if(a==5||a==10) return 2;
if(a==3||a==6||a==9||a==12) return 1;
return 0;This is faster than our other branching methods, sitting at ~4.68 cpu_time, but not fast enough to beat the rest.
Making it branchless:
int a = n%15;
int fiv = a==0 || a==5 || a==10;
int thr = a==0 || a==3 || a==6 ||a==9 || a==12;
return fiv*2+thr;Is actually slower, at ~5.59 cpu_time. I assume this is because it needs to do a==0 twice instead of once?
We can also reduce == by a lot:
int a = n%15;
int fiv = (a-5)*(a-10)*a == 0;
int thr = (a-3)*(a-6)*(a-9)*(a-12)*a == 0;
return fiv*2+thr;but this is way slower, sitting at ~9.00 cpu_time.
Now we've gotten a pretty clear understanding of how fast these tests can go, but there is one last thing we haven't tried:
static int answers[] = {3, 0, 0, 1, 0, 2, 1, 0, 0, 1, 2, 0, 1, 0, 0};
static int FizzBuzzArray(int n){
return answers[n % 15];
}And this is a real gamechanger, sitting at ~2.23 cpu_time. Memory for time tradeoffs are almost always worth it, so default to caching if possible.
To finish it off, here's the graphs over all the tests, first with -O3, then with all functions marked with


Were there any FizzBuzzes I missed? Or any other mistakes? Feel free to comment and correct me. I haven't actually bothered checking if any of the functions work correctly, I just assume they do.
__attribute__((noinline)), and lastly with no optimization at all:


Were there any FizzBuzzes I missed? Or any other mistakes? Feel free to comment and correct me. I haven't actually bothered checking if any of the functions work correctly, I just assume they do.
33
