30
Discussing Bloom Filters
Let's start this blog by discussing a few scenarios and analyzing the search algorithms.


We discussed the scenarios where we can overcome space and time complexities with the help Bloom Filters. Now let's understand what is Bloom Filter.
Bloom Filter is a probabilistic data structure. By probabilistic it means this data structure can the likelihood of an element in a set.
Bloom Filter generates False Positive results which mean it tells if an element is not in a set but isn't sure about if it in the set. It tells either "possibly in the set" or "definitely not in set". Let's demystify it a little bit.
Bloom Filter is a bit array of fixed length. The value of a bit either can be 1 or 0. This bit array is initialized with all bits set to 0. When an element needs to be added, it is passed through a no. of hash functions and the result of each hash function becomes indices of bit array which are then set to 1.
Bloom Filter generates False Positive results which mean it tells if an element is not in a set but isn't sure about if it in the set. It tells either "possibly in the set" or "definitely not in set". Let's demystify it a little bit.
Bloom Filter is a bit array of fixed length. The value of a bit either can be 1 or 0. This bit array is initialized with all bits set to 0. When an element needs to be added, it is passed through a no. of hash functions and the result of each hash function becomes indices of bit array which are then set to 1.
Let's say we have a bit array of length 10.

Let's say we are using 2 hash functions h1 and h2. We receive 2 strings "apple" and "orange".
Suppose,
h1("apple") % 10 = 3
h2("apple") % 10 = 7
h1("apple") % 10 = 3
h2("apple") % 10 = 7
So we will set 3rd and 7th index in array as 1.

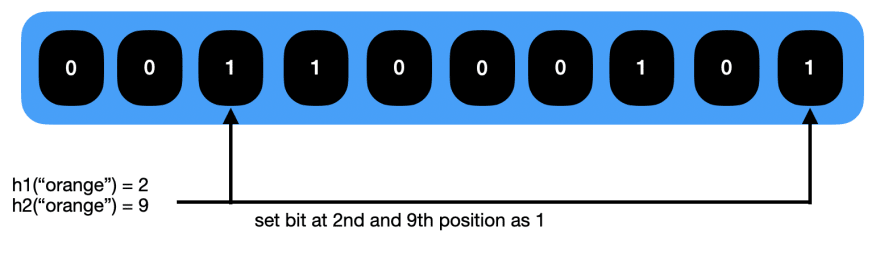
For string "orange", suppose
h1("orange") % 10 = 2
h2("orange") % 10 = 9
h1("orange") % 10 = 2
h2("orange") % 10 = 9
Looking at the current array we can see 2nd and 9th are 0 means no orange string never received otherwise the bit at those index would be 1.
Let's take another example,
We receive "pear" string and suppose
h1("pear") % 10 = 2
h2("pear") % 10 = 5
We receive "pear" string and suppose
h1("pear") % 10 = 2
h2("pear") % 10 = 5
So, hash function h1 for "orange" already set bit at index 2 as 1. But still since we also get index 5 which currently 0, it means we didn't ever receive or stored "pear" before.

Now if we get "apple" again,
h1("apple") % 10 = 2 and h2("apple") % 10 = 9, Since both of these index already set as 1, we do know it already exists in the set.
h1("apple") % 10 = 2 and h2("apple") % 10 = 9, Since both of these index already set as 1, we do know it already exists in the set.
There might be a chance where we get a string even doesn't exist in the set or the storage have indexes received from hash functions as 1 in the bit array. We can certainly reduce the probability of the collisions by
m = - (n lnP)/(ln2)^2
k = (m/n) * ln2
where m is size of bit array,
n is expected number of elements,
P is desired false positive probability,
k is no. of hash functions.
n is expected number of elements,
P is desired false positive probability,
k is no. of hash functions.
30
