32
How to Build a RegEx Engine in Python (Part 3: TDRDP)
In the previous articles we spoke about how to define our grammar, how to build the lexer, and a bit about Python strings.
In this article, we will finally begin the parser, the second-hardest part of the project (the first is the engine).
TDRDP stands for Top-Down Recursive Descent Parsing — a useful technique to create a parser.
I won’t get into the details of when and how you can apply this technique, there’s already plenty of good articles about it, explaining it way better than I could.
Anyway, luckily (😉) the grammar we built in the first article supports it.
To implement a recursive-descent parser, we have to create a function for each non-terminal symbol of the grammar.
So, in our project, a function to parse the RE non-terminal, one for the GROUP, one for the RANGE_EL and so on.
As you noticed, in the techniques’ acronym appear the infamous word ‘recursive’ (and now you’re all scared).
Now you’re probably curious about where the recursion comes up. Well, it turns out the recursion come up in the functions calls:
For example, our grammar has the production rule
RE_SEQ ::= '^'? GROUP ‘$'? ('|' RE_SEQ)? in which two non-terminals appear on the right side, RANGE_EL and RE_SEQ itself. In this case, the function corresponding to the non-terminals RANGE_EL and RE_SEQ itself can be called, hence the recursion.To use TDRDP, once all these functions are created, we call the top-level production, serving as an entry point, which in our case is the one corresponding to the non-terminal RE and the recursive calls will take care of the entire process of parsing by themselves.
At the end, the function we called will return us the result of the parsing, whether it is a boolean, or something more complex like an AST as it is in our case.
The AST, Abstract Syntax Tree, is a tree representation of something, in our case of the regular expression we are parsing.
Quoting Wikipedia: “The syntax is “abstract” in the sense that it does not represent every detail appearing in the real syntax, but rather just the structural or content-related details. For instance, grouping parentheses are implicit in the tree structure, so these do not have to be represented as separate nodes.”
It is composed of nodes in a hierarchy, with a root node at the top:
every node has one parent, except for the root node
nodes can have zero or more children
if a node does not have children, it is called a **leaf **node.

In the above example, we have a regular expression and a possible corresponding AST. The root node is RE, and following the hierarchy to the leaves, you will notice that the leaves have always some letters behind, that are the possible matches for the given element.
You’ll also notice that the left-most leaf letter (A) corresponds to the first letter appearing in the regex, the second with the second, and the right-most leaf with the last one, a range element accepting letters between A and C.
Our goal in the next articles will be to define an AST similar to this, and then to make the parser capable of building it.
Without digging into the details, we can already create a skeleton for our parser.
We’ll start by creating a class called Pyrser (because I’m a funny person) and defining a init method and a parse function, inside which we will define all the functions we need to implement a TDRD parser.
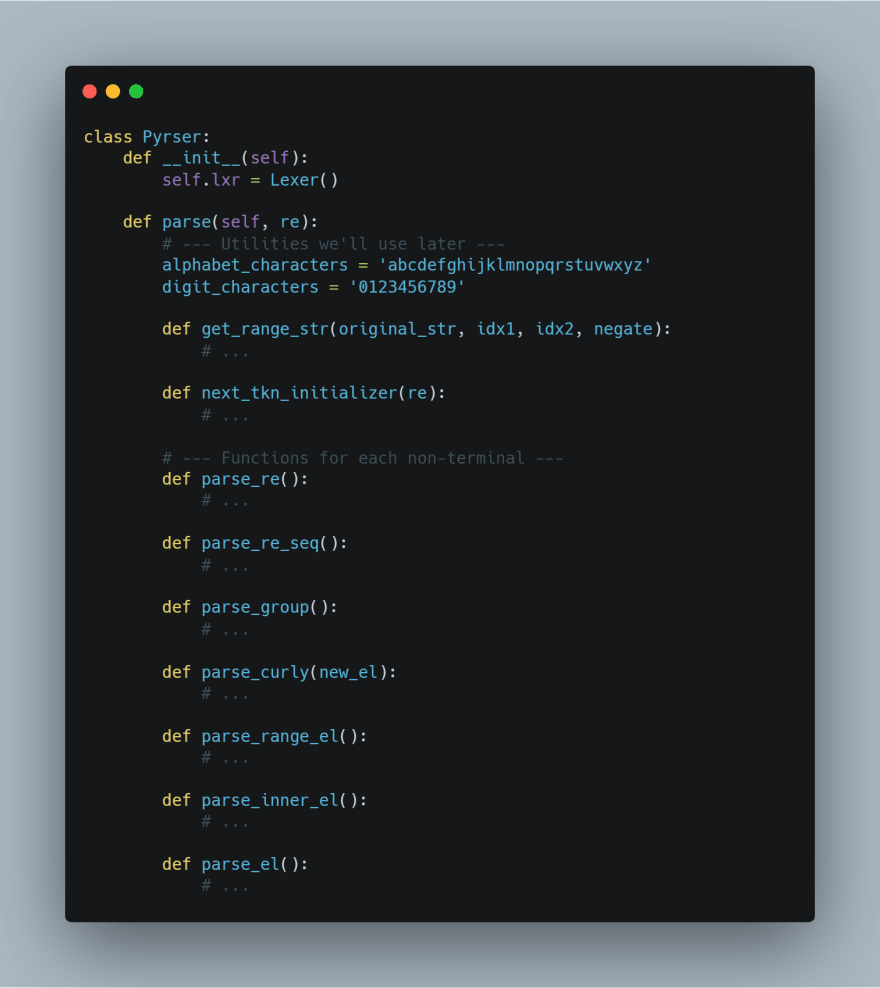
I hope you’re familiar with the concept of closure, because we’re going to use it a lot in our project.
Let’s discuss the utilities first.
We will use the first utility function
get_range_str when we will parse range elements ([a-m|0-3]) to get the number/letters contained in a given range.The second utility
next_tkn_initializer is a closure returning a function that, when called, set the current token to the next one to parse. Although not fundamental, this function is very convenient, as you will notice.As you can see there is a function for each non-terminal of our grammar (except SPECIAL, that was only introduced to denote the special symbols, and QTIFIER that is replaced by parse_curly because the quantifiers
? * + will be parsed inside parse_group for simplicity and the only quantifiers needing a special treatment are only that specified with the curly brace syntax {3} {2,3} {3,} {,3}).Each function of a non-terminal symbol returns an ASTNode object, we will see how it is done in the next article.
For this article, we won’t go deeper into the actual implementation of the parser because we need a good AST implementation first.
Cover Image by Marius Masalar on Unsplash
32
