19
Deep Learning Library From Scratch 2: Backpropagation
Hello and welcome to this second post in this series where we build a deep learning library from scratch.
The code for this blog series can be found in this Github repo.
Please also look at my Github profile and star anything you like or give feedback on how I can improve.
In the last post (found here), we implemented linear layers and common activation functions, and successfully built the forward pass of the neural network.
So far, our model can only make predictions, but has no facility to train and correct its predictions. This is what we will be covering today by implementing a process called backpropagation.
When a neural network trains, it is given a dataset with inputs and their corresponding output.
The network would produce its prediction from the dataset's input and calculate how far away its prediction is from the real output given in the dataset (this is called the loss).
The aim of training a neural network is to minimise this loss.
After the loss is calculated, the weights and biases of the network are tweaked in such a way that it reduces the loss value. Remember in the previous post, weights and biases are our adjustable network parameters, which are used in the calculation of the network output.
This process repeats several number of times, with the loss hopefully decreasing with each repetition. Each repetition is known as an epoch.
There are many different loss functions, however we will only look at the Mean Squared Error function in this post. More loss functions will be look at in future posts.
Loss functions receive the raw error of the network (which is calculated with predicted outputs - actual outputs) and produce a measurement of how bad the error is.
Mean Squared Error (MSE) takes the error vector and returns the mean of all the squared values in the vector.
For example...
Network output: [1, 2, 3]
Actual outputs: [3, 2, 1]
Error: [-2, 0, 2]
Loss: 2.6666666 ( ( (-2)**2 + (0)**2 + (2)**2 ) / 3 )The reason why you square the errors first, instead of calculating the mean immediately is so that any negative values in the error vector are treated the same as positive values in the error vector (since a negative number squared is positive).
Here is the our python class for MSE...
#loss.py
import numpy as np
class MSE:
def __call__(self, pred, y):
self.error = pred - y
return np.mean(self.error ** 2)Backpropagation is the training process of the network.
The aim of the neural network training process is to minimise the loss.
This can be treated as an optimisation problem, whose solutions rely heavily on calculus - differentiation to be more specific.
The first step in backpropagation is to find the gradient of all the weights and biases in the network, with respect to the loss function.
Let's use an example to demonstrate...
Our small example network consist of
1 Linear layer
1 Sigmoid layerSo the whole network's output calculation will be as such...
x - the network input
w - the linear layer's weight
b - the linear layer's bias
a - linear layer output
pred - network output / sigmoid output
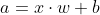
Now let's calculate the loss
y - the expected output for x
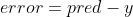
Now we have to find the gradient of the weights/biases with respect to the loss
This step utilises the chain rule
We have now calculated the gradients of the parameters with respect to the loss.
The general rule for calculating the gradient weights/biases of a certain layer with respect to the loss is...
Differentiate each layer's output with respect to it's input (starting from the last layer till you reach the layer whose parameters you want to adjust)
Multiply all those results together and call this grad
Once you have reached the desired layer, differentiate its output with respect to its weight (call this w_grad) and differentiate with respect to its bias (call this b_grad).
Multiply w_grad and grad to get the gradient of loss with respect to the layer's weight. Do the same with b_grad, to get the gradient of loss with respect to the layer's bias.
With this in mind, here is the code for all our layers and MSE.
#loss.py
import numpy as np
class MSE:
def __call__(self, pred, y):
self.error = pred - y
return np.mean(self.error ** 2)
def backward(self):
return 2 * (1 / self.error.shape[-1]) * self.error#layers.py
import numpy as np
class Activation:
def __init__(self):
pass
class Layer:
def __init__(self):
pass
class Model:
def __init__(self, layers):
self.layers = layers
def __call__(self, x):
output = x
for layer in self.layers:
output = layer(output)
return output
class Linear(Layer):
def __init__(self, units):
self.units = units
self.initialized = False
def __call__(self, x):
self.input = x
if not self.initialized:
self.w = np.random.rand(self.input.shape[-1], self.units)
self.b = np.random.rand(self.units)
self.initialized = True
return self.input @ self.w + self.b
def backward(self, grad):
self.w_gradient = self.input.T @ grad
self.b_gradient = np.sum(grad, axis=0)
return grad @ self.w.T
class Sigmoid(Activation):
def __call__(self, x):
self.output = 1 / (1 + np.exp(-x))
return self.output
def backward(self, grad):
return grad * (self.output * (1 - self.output))
class Relu(Activation):
def __call__(self, x):
self.output = np.maximum(0, x)
return self.output
def backward(self, grad):
return grad * np.clip(self.output, 0, 1)
class Softmax(Activation):
def __call__(self, x):
exps = np.exp(x - np.max(x))
self.output = exps / np.sum(exps, axis=1, keepdims=True)
return self.output
def backward(self, grad):
m, n = self.output.shape
p = self.output
tensor1 = np.einsum('ij,ik->ijk', p, p)
tensor2 = np.einsum('ij,jk->ijk', p, np.eye(n, n))
dSoftmax = tensor2 - tensor1
dz = np.einsum('ijk,ik->ij', dSoftmax, grad)
return dz
class Tanh(Activation):
def __call__(self, x):
self.output = np.tanh(x)
return self.output
def backward(self, grad):
return grad * (1 - self.output ** 2)The backward method in each class is a function that differentiates the layer's output with respect to its input.
Feel free to look up each of the activation function's derivates, to make the code make more sense.
The backward function for the linear layer is different, since it not only calculates the gradient of the output with respect to the input, but to its parameters too.
The differentiation rule for matrix multiplication is as follows, where x and y are matrices being multiplied together
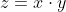
There are many ways of optimising network parameters, but in this post we will cover the most basic method which is Stochastic Gradient Descent (SGD).
SGD is very simple. It takes each parameter's calculated gradient and multiplies it by a specified learning rate. The respective parameter is then subtracted by this result.
The reason why a learning rate is used is to control how fast the network learns.
The best learning rate value minimises the cost in a small number of epochs.
A too small learning rate minimises the cost too, but after several epochs, so would take time.
A too large learning rate would make the loss approach a value which is not its minimum, so the network fails to train properly.
Here is the code for MSE
#optim.py
import layers
import tqdm
#tqdm is a progress bar, so we can see how far into the epoch we are
class SGD:
def __init__(self, lr = 0.01):
self.lr = lr
def __call__(self, model, loss):
grad = loss.backward()
for layer in tqdm.tqdm(model.layers[::-1]):
grad = layer.backward(grad) #calculates layer parameter gradients
if isinstance(layer, layers.Layer):
layer.w -= layer.w_gradient * self.lr
layer.b -= layer.b_gradient * self.lrWith all things in place to train the network, we can add a train function to our model.
#layers.py
import numpy as np
import loss
import optim
np.random.seed(0)
#...
class Model:
def __init__(self, layers):
self.layers = layers
def __call__(self, x):
output = x
for layer in self.layers:
output = layer(output)
return output
def train(self, x, y, optim = optim.SGD(), loss=loss.MSE(), epochs=10):
for epoch in range(1, epochs + 1):
pred = self.__call__(x)
l = loss(pred, y)
optim(self, loss)
print (f"epoch {epoch} loss {l}")
#...We are going to build and train a neural network so that it can perform as an XOR gate.
XOR gates take in two inputs. The inputs can either be 0 or 1 (representing False or True)
If both the inputs are the same, the gate outputs 0.
If both the inputs are not the same, the gate outputs 1.
#main.py
import layers
import loss
import optim
import numpy as np
x = np.array([[0, 1], [0, 0], [1, 1], [0, 1]])
y = np.array([[1],[0],[0], [1]])
net = layers.Model([
layers.Linear(8),
layers.Relu(),
layers.Linear(4),
layers.Sigmoid(),
layers.Linear(1),
layers.Sigmoid()
])
net.train(x, y, optim=optim.SGD(lr=0.6), loss=loss.MSE(), epochs=400)
print (net(x))Output
...
epoch 390 loss 0.0011290060124405485
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 391 loss 0.0011240809175767955
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 392 loss 0.0011191976855805586
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 393 loss 0.0011143557916784605
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 394 loss 0.0011095547197546522
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 395 loss 0.00110479396217416
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 396 loss 0.0011000730196106248
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 397 loss 0.0010953914008780786
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 398 loss 0.0010907486227668803
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 399 loss 0.0010861442098835058
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 400 loss 0.0010815776944942087
[[0.96955654]
[0.03727081]
[0.03264158]
[0.96955654]]As you can see, the result is really good and not too far off from the real outputs (a loss of 0.001 is really low).
We can also adjust our model to work with other activation functions
#main.py
import layers
import loss
import optim
import numpy as np
x = np.array([[0, 1], [0, 0], [1, 1], [0, 1]])
y = np.array([[0, 1], [1, 0], [1, 0], [0, 1]])
net = layers.Model([
layers.Linear(8),
layers.Relu(),
layers.Linear(4),
layers.Sigmoid(),
layers.Linear(2),
layers.Softmax()
])
net.train(x, y, optim=optim.SGD(lr=0.6), loss=loss.MSE(), epochs=400)
print (net(x))Output
epoch 390 loss 0.00045429759266240227
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 391 loss 0.0004524694487356741
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 392 loss 0.000450655387643655
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 393 loss 0.00044885525012255907
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<00:00, 6236.88it/s]
epoch 394 loss 0.00044706887927775473
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 395 loss 0.0004452961205401462
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<00:00, 5748.25it/s]
epoch 396 loss 0.0004435368216234964
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 397 loss 0.00044179083248269265
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 398 loss 0.00044005800527292425
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 399 loss 0.00043833819430972714
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6/6 [00:00<?, ?it/s]
epoch 400 loss 0.0004366312560299245
[[0.01846441 0.98153559]
[0.97508489 0.02491511]
[0.97909267 0.02090733]
[0.01846441 0.98153559]]Wow! We have successfully built a working neural network. This can be successfully applied to more useful things, such as the MNIST dataset, which we will use soon in another post.
The next post will go through more loss functions and more optimisation functions.
Thanks for reading!
19