Your complete guide to Heap data structure!

Hi, I'm Aya Bouchiha, in this beautiful day, I'm going to explain the Heap data structure.
#day_22

Definition of Heap

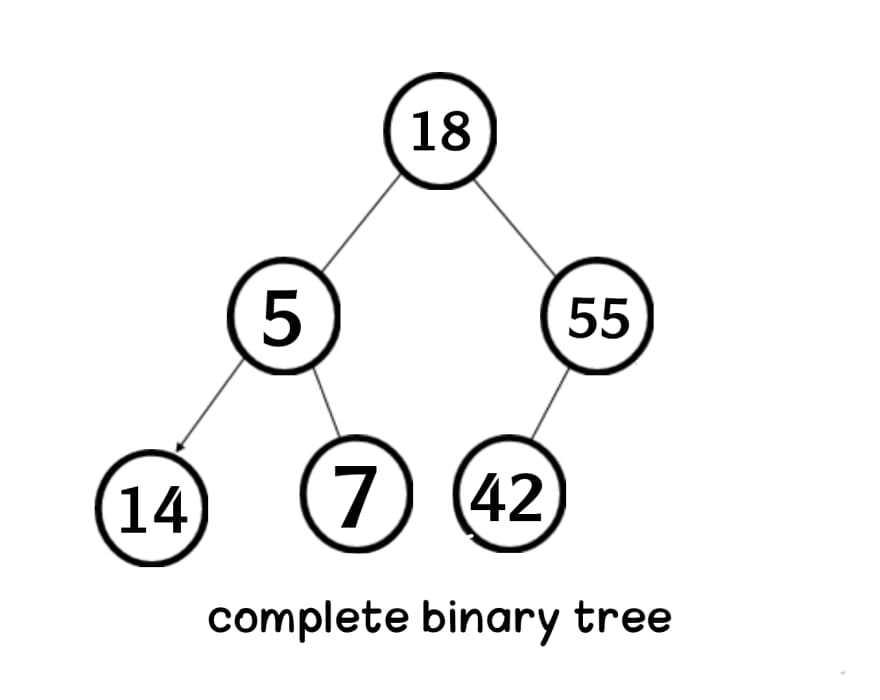
Heap: is a complete binary tree (types of a binary tree) (which each node has at most two children and All the leaves should lean towards the left) where the root node is compared with its children and arrange accordingly.

Example of complete binary tree

Example of incomplete binary tree

Types of Heap

1. Max-heap

The key of every node is smaller than or equal its parent

arr[parent] >= arr[i]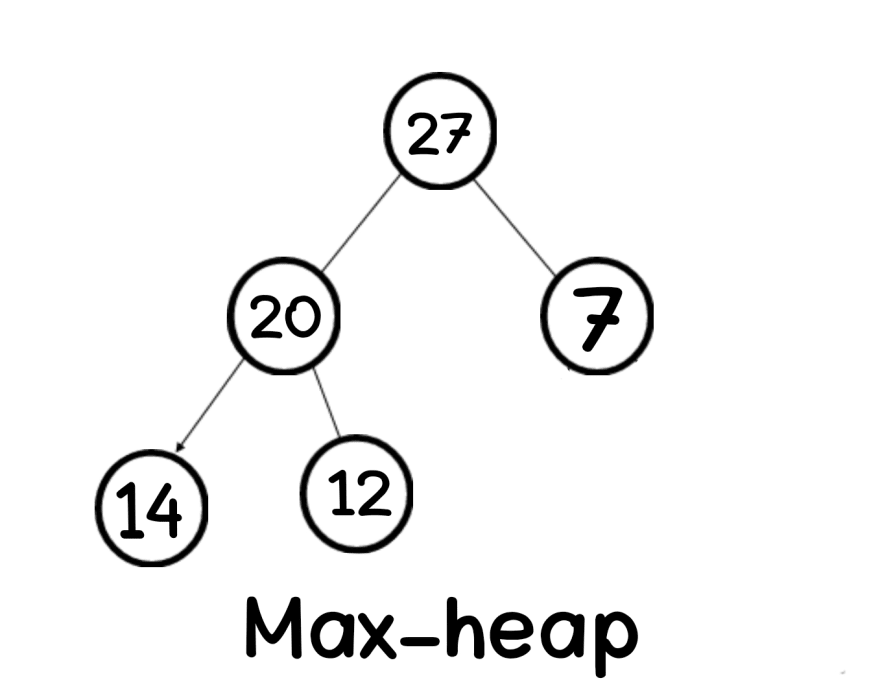

Example of max-heap

2. Min-heap

The key of every node is greater than or equal its parent

arr[parent] <= arr[i]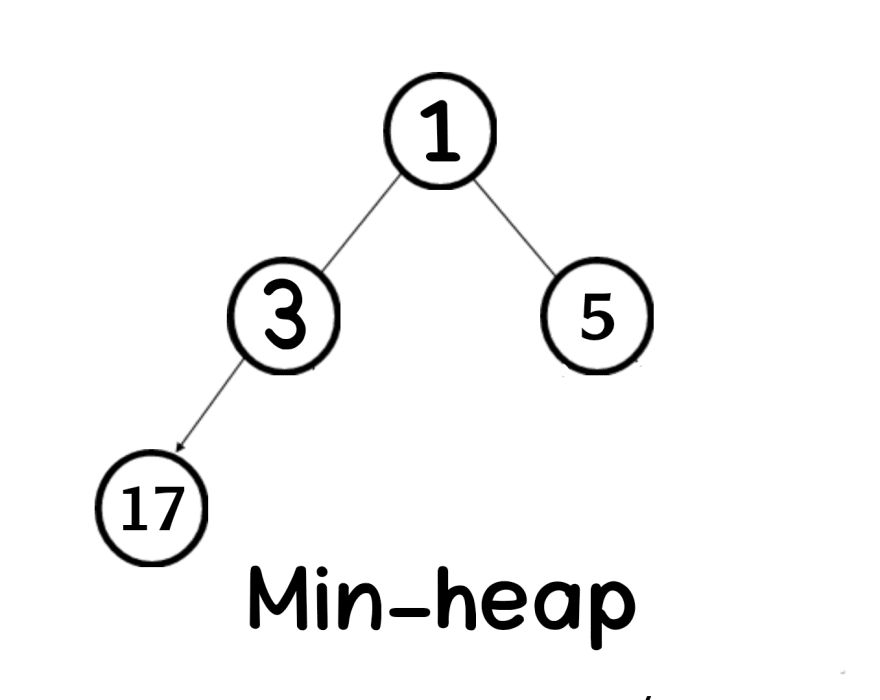

Example of min-heap

Application of Heap

  • Heap sort algorithm
  • Order statistics Getting The minimum value or the maximum value in a constant time
  • Graph algorithms like Prim's Algorithm and Dijkstra's algorithm
  • Priority Queue

Space and Time complexity of Heap

The space complexity of the heap is O(n)

insertion (push) deletion (pop) peek
O(log n) O(log n) O(1)

Heap array implementation

let's take this example of max-heap:
the index of each node is between parentheses ( ):

15(0)
      /          \
 (1) 9            13 (2)
    /  \         /
(3)5  (4)7   (5)11
arr = [15, 9, 13, 5, 7, 11]

the implementation can be done by:

  • making the root the first element in the array arr[0] = root
  • Parent node: arr[(i - 1) // 2]
  • Left-child: arr[2 * i + 1]
  • Right-child: arr[2 * i + 2] 
class MinHeap:
    def __init__(self):
        self.heap = []
        self.heap_size = 0

    def getParentNodeIndex(self, i: int) -> int:
        return (i-1)//2

    def getLeftChildNodeIndex(self, i: int) -> int:
        return 2*i+1

    def getRightChildNodeIndex(self, i: int) -> int:
        return 2*i+2

    def hasParent(self, i: int) -> bool:
        # cheking if a node has a parent
        return self.getParentNodeIndex(i) < len(self.heap)

    def hasLeftChild(self, i: int) -> bool:
        # cheking if a node has a left child
        return self.getLeftChildNodeIndex(i) < len(self.heap)

    def hasRightChild(self, i: int) -> bool:
        # cheking if a node has a right child
        return self.getRightChildNodeIndex(i) < len(self.heap)

    def getMinValue(self) -> int:
        """
            time complexity => O(1)
        """
        return self.heap[0]

    def printAll(self):
        print(self.heap)

Insertion (push) in Heap

1. Approach of insertion

  • Increase the size of the heap to add a new element
  • The heap is a complete binary tree that's why the new element should lean towards the left, which means, in array representation, we insert the element at the end of the array.
  • Heap must satisfy the heap-order property, that's why we should Heapify or bubble up the new element, Heapify or bubbling up is swapping the new element with its parent until
    • its parent is greater than or equal to it in a max-heap.
    • its parent is smaller than or equal to it in min-heap.

1. Explanation of insertion

For better understanding, let's take an example:
  we want to insert 1 in this min-heap

3 (0)
      /   \
 (1) 5     10 (2)
   / 
  9 (3)
[3, 5, 10, 9]
  1. Insert the new Element at the end of the array 
3 (0)
       /   \
 (1)  5     10 (2)
    /  \ 
(3)9 (4)1
heap_size += 1
  arr = [3, 5, 10, 9, 1]
  1. Bubble up the new element
  • Since 1 < 5, swap them, so: 
3 (0)
       /   \
 (1)  1     10 (2)
    /  \ 
(3)9 (4)5
arr = [3, 5, 10, 9, 1]
  newElementIndex = len(arr) - 1 # 4
  # the index of the parent of the new element
  ParentIndex = (newElementIndex - 1) // 2 # (4-1)//2 = 1 
  # 1 < 5 
  if arr[newElementIdx] < arr[ParentIdx]:
      # swap(1, 5)
      arr[newElementIdx], arr[ParentIdx] = arr[ParentIdx], arr[newElementIdx]

the array will be:

arr = [3, 1, 10, 9, 5]
  • Hence 1 < 3, swap them, so: 
1 (0)
       /   \
 (1)  3     10 (2)
    /  \ 
(3)9 (4)5

we'll do the same process for 1 and 3 like (1 and 5) so the array will be

arr = [1, 3, 10, 9, 5]

3. Implementation of insertion in python

the implementation of bubble up or heapify function in python 

def bubbleUp(self, i: int):
        parentIndex = self.getParentNodeIndex(i)
        if parentIndex < 0:
            parentIndex = 0 
        # Loops until it reaches a leaf node
        while(i > 0 and self.heap[i] < self.heap[self.getParentNodeIndex(i)]): 
            # Swap the elements
            self.heap[i], self.heap[self.getParentNodeIndex(i)] = self.heap[self.getParentNodeIndex(i)], self.heap[i]
            i = self.getParentNodeIndex(i)

the implementation of insert function in python 

def insert(self, value: int):
        self.heap_size += 1
        # insert the element at the end
        self.heap.append(value) 
        # bubble up the new element
        self.bubbleUp(len(self.heap) - 1)

Deletion in Heap

1. Approach of Deletion

The standard deletion operation on Heap is deleting the root which is the maximum value of the max-heap, and the minimum value of the in-heap.

  • Decrease the size of the heap to delete the element
  • Swap the root with the last element
  • Pop (delete) last element of the array
  • Heap must satisfy the heap-order property, that's why we should bubble-down (also known as heapify, percolate-down, sift-down, sink-down, trickle-down, heapify-down, cascade-down, extract-min or extract-max, or down-heap) the new element, bubble-down is swapping the new element with one of its children until
    • the child is smaller than or equal to it in a max-heap.
    • the child is greater than or equal to it in a min-heap.

1. Explanation of deletion

For better understanding, let's take an example:
  we want to delete 3 in this min-heap

3 (0)
      /   \
 (1) 5     10 (2)
   / 
  9 (3)
[3, 5, 10, 9]
  1. Swap the root with the last element 
9 (0)
       /   \
 (1)  5     10 (2)
    /  
(3)3
arr = [9, 5, 10, 3]
  1. Delete the last element and decrease the size of the array 
9 (0)
       /   \
 (1)  5     10 (2)
arr = [9, 5, 10, 3]
  heap_size -= 1
  arr.pop()

so the array will be

arr = [9, 5, 10]
  1. Bubble down the root
  • Since 9 > 5, swap them, so: 
5 (0)
       /   \
 (1)  9     10 (2)
arr = [5, 9, 10]

3. Implementation of deletion in python

Bubble down implementation in python 

def bubbleDown(self):
        # the index of the root => 0
        i = 0
        while True:
            smallest = None

            leftChildIndex = self.getLeftChildNodeIndex(i)
            rightChildIndex =  self.getRightChildNodeIndex(i)
            #  if the node has not any child 
            if (not self.hasLeftChild(i) and not self.hasRightChild(i)):
                break
            # if the node has only a left child
            elif (not self.hasRightChild(i)):
                # the smallest variable will be the index of the left child
                smallest = leftChildIndex
            # if the node has only a right child
            elif (not self.hasLeftChild(i)):
                # the smallest variable will be the index of the right child
                smallest = rightChildIndex
            # if the node has 2 children
            else:
                # the smallest variable will be the smallest value of the 2 children
                smallest = rightChildIndex if self.heap[rightChildIndex] < self.heap[leftChildIndex] else leftChildIndex            
            # if the node's value is greater than its one of children
            if (self.heap[i] > self.heap[smallest]):
                # swap the node with its child
                self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
                # the i variable will be the index of the smallest value of the two children
                i = smallest
            # if the node's value is smaller than its one of children
            else:
                break
        return

delete implementation in python 

def delete(self):
        # if the size the heap is one or the heap is empty(size = 0)
        if self.heap_size <= 1:
            self.heap = []
            return
        # replace last element with the root
        self.heap[self.heap_size - 1], self.heap[0] = self.heap[0], self.heap[self.heap_size - 1]
        # decrease the size of heap
        self.heap_size -= 1
        # delete last element
        self.heap.pop()
        self.bubbleDown()

Heap implementation in python (Final code) 

class MinHeap:
    def __init__(self):
        self.heap = []
        self.heap_size = 0

    def getParentNodeIndex(self, i: int) -> int:
        return (i-1)//2

    def getLeftChildNodeIndex(self, i: int) -> int:
        return 2*i+1

    def getRightChildNodeIndex(self, i: int) -> int:
        return 2*i+2

    def hasParent(self, i: int) -> bool:
        # cheking if a node has a parent
        return self.getParentNodeIndex(i) < len(self.heap)

    def hasLeftChild(self, i: int) -> bool:
        # cheking if a node has a left child
        return self.getLeftChildNodeIndex(i) < len(self.heap)

    def hasRightChild(self, i: int) -> bool:
        # cheking if a node has a right child
        return self.getRightChildNodeIndex(i) < len(self.heap)

    def getMinValue(self) -> int:
        """
            time complexity => O(1)
        """
        return self.heap[0]

    def insert(self, value: int):
        self.heap_size += 1
        # insert the element at the end
        self.heap.append(value) 
        # bubble up the new element
        self.bubbleUp(len(self.heap) - 1)

    def bubbleUp(self, i: int):
        parentIndex = self.getParentNodeIndex(i)
        if parentIndex < 0:
            parentIndex = 0 
        # Loops until it reaches a leaf node
        while(i > 0 and self.heap[i] < self.heap[self.getParentNodeIndex(i)]): 
            # Swap the elements
            self.heap[i], self.heap[self.getParentNodeIndex(i)] = self.heap[self.getParentNodeIndex(i)], self.heap[i]
            i = self.getParentNodeIndex(i) 

    def delete(self):
        # if the size the heap is one or the heap is empty(size = 0)
        if self.heap_size <= 1:
            self.heap = []
            return
        # replace last element with the root
        self.heap[self.heap_size - 1], self.heap[0] = self.heap[0], self.heap[self.heap_size - 1]
        # decrease the size of heap
        self.heap_size -= 1
        # delete last element
        self.heap.pop()
        self.bubbleDown()

    def bubbleDown(self):
        # the index of the root => 0
        i = 0
        while True:
            smallest = None

            leftChildIndex = self.getLeftChildNodeIndex(i)
            rightChildIndex =  self.getRightChildNodeIndex(i)
            #  if the node has not any child 
            if (not self.hasLeftChild(i) and not self.hasRightChild(i)):
                break
            # if the node has only a left child
            elif (not self.hasRightChild(i)):
                # the smallest variable will be the index of the left child
                smallest = leftChildIndex
            # if the node has only a right child
            elif (not self.hasLeftChild(i)):
                # the smallest variable will be the index of the right child
                smallest = rightChildIndex
            # if the node has 2 children
            else:
                # the smallest variable will be the smallest value of the 2 children
                smallest = rightChildIndex if self.heap[rightChildIndex] < self.heap[leftChildIndex] else leftChildIndex            
            # if the node's value is greater than its one of children
            if (self.heap[i] > self.heap[smallest]):
                # swap the node with its child
                self.heap[i], self.heap[smallest] = self.heap[smallest], self.heap[i]
                # the i variable will be the index of the smallest value of the two children
                i = smallest
            # if the node's value is smaller than its one of children
            else:
                break
        return

    def printAll(self):
        print(self.heap)

my_heap = MinHeap()
my_heap.insert(5)
my_heap.insert(10)
my_heap.insert(1)
my_heap.insert(2)
my_heap.insert(3)
my_heap.insert(4)
#      1
#    /  \ 
#   2     4
#  / \   /
# 10  3  5
my_heap.printAll()
my_heap.delete()
my_heap.printAll()
#      2
#    /  \ 
#   3     4
#  / \   
# 10  5  
print(my_heap.heap_size) # 5
print(my_heap.getMinValue()) # 2

References and useful resources

if you have any suggestions for the next posts or any questions you can contact me in telegram

Happy coding :)
#day_22

13

Tags:

AlgorithmsComputerscienceCodenewbieBeginners