Representation of Graph

Hello, in this post we'll discuss the representations of a graph, their characteristics, space complexity, and also their implementation in python.

1. Adjacency matrix

in this type of representation, we use 2-dimensional arrays to represent the graph where the number of columns and rows is the total number of vertices.

if A[i][j] = 1 that means i and j are adjacent.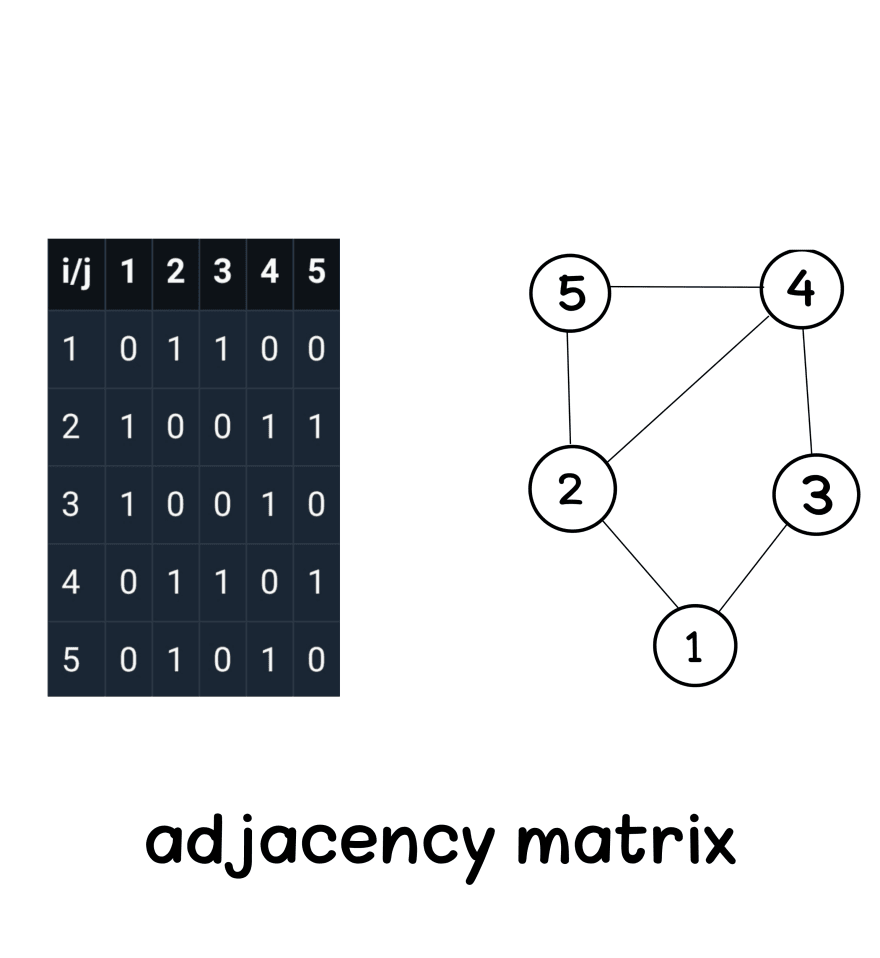

characteristics of using adjacency matrix

Fast to lookup and check for presence or absence of a specific edge between any two nodes O(1)

Fast to add a new edge O(1)

Slow to iterate over all edges

Slow to add or delete a node O(n²)

Space complexity of adjacency matrix

The space complexity of adjacency matrix is O(n²)

Example of the adjacency matrix

Implementation Of Adjacency matrix in python

class Graph():
    def __init__(self, matrixSize):
        # fill the matrix with 0.
        self.adjacencyMatrix = []
        for i in range(matrixSize):
            self.adjacencyMatrix.append([0 for i in range(matrixSize)])
        self.matrixSize = matrixSize

    def addEdge(self, node1, node2):
        self.adjacencyMatrix[node1][node2] = 1
        self.adjacencyMatrix[node2][node1] = 1

    def deleteEdge(self, node1, node2):
        # if there is an edge between the two giving nodes
        if self.adjacencyMatrix[node1][node2] == 1 :
            self.adjacencyMatrix[node1][node2] = 0
            self.adjacencyMatrix[node2][node1] = 0

2. Adjacency List

The adjacency list is represented as an array of linked lists, where each index of the array represents a node and each node represents its adjacents nodes using a linked list.

characteristics of adjacency list

Memory usage depends on the number of edges (not the number of nodes) which might save a lot of memory

slower than matrix for checking the presence or the absence of an edges

Fast to iterate over all edges

Space of complexity of adjacency list

The space complexity of the adjacency list is O(|V|+|E|).

Example of adjacency list

Implementation of adjacency list

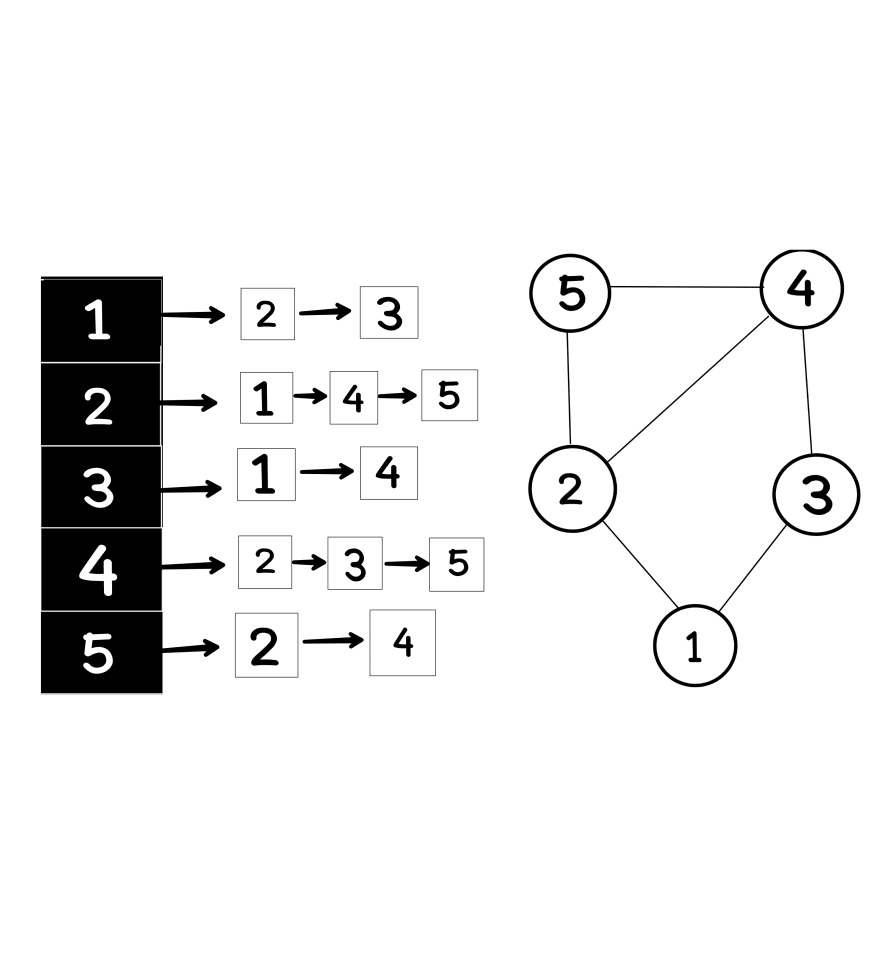
class AdjNode:
    def __init__(self, data):
        self.vertex = data
        self.next = None


# A class to represent a graph. A graph
# is the list of the adjacency lists.
# Size of the array will be the no. of the
# vertices "V"
class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = [None] * self.V

    # Function to add an edge in an undirected graph
    def add_edge(self, src, dest):
        # Adding the node to the source node
        node = AdjNode(dest)
        node.next = self.graph[src]
        self.graph[src] = node

        # Adding the source node to the destination as
        # it is the undirected graph
        node = AdjNode(src)
        node.next = self.graph[dest]
        self.graph[dest] = node

    # Function to print the graph
    def print_graph(self):
        for i in range(self.V):
            print("Adjacency list of vertex {}\n head".format(i), end="")
            temp = self.graph[i]
            while temp:
                print(" -> {}".format(temp.vertex), end="")
                temp = temp.next
            print(" \n")