A gentle introduction to Reinforcement Learning

In 2016, AplhaGo, a program developed for playing the game of Go, made headlines when it beat the world champion Go player in a five-game match. It was a remarkable feat because the number of possible legal moves in Go is of the order of 2.1 × 10¹⁷⁰. To put this in context, this number is far, far greater than the number of atoms in the observable universe, which are of the order of 10⁸⁰. Such a high number of possibilities make it almost impossible to create a program that can play effectively using brute-force or somewhat optimized search algorithms.

A part of the secret sauce of AlphaGO was the usage of Reinforcement Learning to improve its understanding of the game by playing against itself. Since then, the field of Reinforcement Learning has seen increased interest, and much more efficient programs have been developed to play various games at a pro-human efficiency. Although you would find Reinforcement Learning discussed in the context of Games and Puzzles in most places (including this post), the applications of Reinforcement Learning are much more expansive. The objective of this tutorial is to give you a gentle introduction to the world of Reinforcement Learning.

ℹ️ First things first! This post was written in collaboration with Alexey Vinel (Professor, Halmstad University). Some ideas and visuals are borrowed from my previous post on Q-learning written for Learndatasci. Unlike most posts you'll find on Reinforcement learning, we try to explore Reinforcement Learning here with an angle of multiple agents. So this makes it slightly more complicated and exciting at the same time. While this will be a good resource to develop an intuitive understanding of Reinforcement Learning (Reinforcement Q-learning, to be specific), it is highly recommended to visit the theoretical parts (some links shared in the appendix) if you're willing to explore Reinforcement Learning beyond this post.

I had to fork openAI's gym library to implement a custom environment. The code can be found on this GitHub repository. If you'd like to explore an interactive version, you can check out this google colab notebook. We use Python to implement the algorithms; if you're not familiar with Python, you can pretend that those snippets don't exist and read through the textual part (including code comments). Alright, time to get started 🚀

What is Reinforcement Learning?

Reinforcement learning is a paradigm of Machine Learning where learning happens through the feedback gained by an agent's interaction with its environment. This is also one of the critical differentiators of Reinforcement Learning with the other two paradigms of Machine learning (Supervised learning and Unsupervised learning). Supervised learning algorithms require fully labelled training data, and Unsupervised learning algorithms need no labels. On the other hand, Reinforcement learning algorithms utilize feedback from the environment they're operating in to get better at the tasks they're being trained to perform. So we can say that Reinforcement Learning lies somewhere in the middle of the spectrum.

It is inevitable to talk about Reinforcement Learning with clarity without using some technical terms like "agent", "action", "state", "reward", and "environment". So let's try to gain a high-level understanding of Reinforcement Learning and these terms through an analogy,

Understanding Reinforcement learning through Birding

Let's watch the first few seconds of this video first,

Pretty cool, isn't it?

And now think about how did someone manage to teach this parrot to reply with certain sounds on specific prompts. And if you carefully observed, part of the answer lies in the parrot's food after every cool response. The human asks a question, and the parrot tries to respond in many different ways, and if the parrot's response is the desired one, it is rewarded with food. Now guess what? The next time the parrot is exposed to the same cue, it is likely to answer similarly, expecting more food. This is how we "reinforce" certain behaviours through positive experiences. If I had to explain the above process in terms of Reinforcement learning concepts, it'd be something like,

"The agent learns to take desired for a given state in the environment",

where,

• The "agent" is the parrot
• The "state" is questions or cues the parrot is exposed to
• The "actions" are the sounds it is uttering
• The "reward" is the food he gets when he takes the desired action
• And the "environment" is the place where the parrot is living (or, in other words, everything else than the parrot)

Reinforcement can happen through negative experiences too. For example, if a child touches a burning candle out of curiosity, (s)he is unlikely to repeat the same action. So, in this case, instead of a reward, the agent got a penalty, which would disincentivize the agent to repeat the same action in future again.

If you try to think about it, there are countless similar real-world analogies. This suggests why Reinforcement Learning can be helpful for a wide variety of real-world applications and why it might be a path to create General AI Agents (think of a program that can not just beat a human in the game of Go, but multiple games like Chess, GTA, etc.). It might still take a lot of time to develop agents with general intelligence, but reading about programs like MuZero (one of the many successors of Alpha Go) hints that Reinforcement learning might have a decent role to play in achieving that.

After reading the analogies, a few questions like below might have come into your mind,

• Real-world example is fine, but how do I do this "reinforcement" in the world of programs?
• What are these algorithms, and how do they work?

Let's start answering such questions as switch gears and dive into certain technicalities of Reinforcement learning.

Example problem statement: Self-driving taxi

Wouldn't it be fantastic to train an agent (i.e. create a computer program) to pick up from a location and drop them at their desired location? In the rest of the tutorial, we'll solve a simplified version of this problem through reinforcement learning.

Let's start by specifying typical steps in a Reinforcement learning process,

1. Agent observes the environment. The observation is represented in digital form and also called "state".
2. The agent utilizes observation to decide how to act. The strategy agent uses to figure out the action to perform is also referred to as "policy".
3. The agent performs the action in the environment.
4. The environment, as a result of the action, may move to a new state (i.e. generate different observations) and may return feedback to the agent in the form of rewards/penalties.
5. The agent uses rewards and penalties to refine its policy.
6. The process can be repeated until the agent finds an optimal policy.

Now that we're clear about the process, we need to set up the environment. In most cases, what this means is we need to figure out the following details,

1. The state-space

Typically, a "state" will encode the observable information that the agent can use to learn to act efficiently. For example, in the case of self-driving-taxi, the state information could contain the following information,

• The current location of the taxi
• The current location of the passenger
• The destination

There can be multiple ways to represent such information, and how one ends up doing it depends on the level of sophistication intended.

The state space is the set of all possible states an environment can be in. For example, if we consider our environment for the self-driving taxi to be a two-dimensional 4x4 grid, there are

• 16 possible locations for the taxi
• 16 possible locations for the passenger
• and 16 possible destination

This means our state-space size becomes 16 x 16 x 16 = 4096, i.e. at any point in time, the environment must be in either of these 4096 states.

2. The action space

Action space is the set of all possible actions an agent can take in the environment. Taking the same 2D grid-world example, the taxi agent may be allowed to take the following actions,

• Move North
• Move South
• Move East
• Move West
• Pickup
• Drop-off

Again, there can be multiple ways to define the action space, and this is just one of them. The choice also depends on the level of complexity and algorithms you'd want to use later.

3. The rewards

The rewards and penalties are critical for an agent's learning. While deciding the reward structure, we must carefully think about the magnitude, direction (positive or negative), and the reward frequency (every time step / based on specific milestone / etc.). Taking the same grid environment example, some ideas for reward structure can be,

• The agent should receive a positive reward when it performs a successful passenger drop-off. The reward should be high in magnitude because this behaviour is highly desired.
• The agent should be penalized if it tries to drop off a passenger in the wrong locations.
• The agent should get a small negative reward for not making it to the destination after every step. This would incentivize the agent to take faster routes.

There can be more ideas for rewards like giving a reward for successful pickup and so on.

4. The transition rules

The transition rules are kind of the brain of the environment. They specify the dynamics of the above-discussed components (state, action, and reward). They are often represented in terms of tables (a.k.a state transition tables) which specify that,

For a given state S, if you take action A, the new state of the environment becomes S', and the reward received is R.

An example row could be when the taxi's location is in the middle of the grid, the passenger's location in the bottom-right corner. The agent takes the "Move North" action, it gets a negative reward, and the next state becomes the state representing the taxi in its new position.

Note: In the real world, the state transitions may not be deterministic, i.e. they can be either.

• Stochastic; which means the rules operate by probability, i.e. if you take action, there's an X₁% chance you'll end up in state S₁, and Xn% chance you'd end up in a state Sn.
• Unknown, which means it is not known in advance what all possible states the agent can get into if it takes action A in a given state S. This might be the case when the agent is operating in the real world.

Implementing the environment

Implementing a computer program that represents the environment can be a bit of a programming effort. Apart from deciding the specifics like the state space, transition table, reward structure, etc., we need to implement other features like creating a way to input actions into the environment and getting feedback in return. More often than not, there's also a requirement to visualize what's happening under the hood. Since the objective of this tutorial is "Introduction to Reinforcement Learning", we will skip the "how to program a Reinforcement learning environment" part and jump straight to using it. However, if you're interested, you can check the source code and follow the comments there.

Specifics of the environment

We'll use a custom environment inspired by OpenAI gym's Taxi-v3 environment. We have added a twist to the environment. Instead of having a single taxi and a single passenger, we'll be having two taxis and a passenger! The intention behind the mod is to observe interesting dynamics that might arise because of the presence of another taxi. This also means the state space would comprise an additional taxi location, and the action space would comprise of actions of both the taxis now.

Our environment is built on OpenAI's gym library, making it convenient to implement environments to evaluate Reinforcement learning algorithms. They also include some pre-packaged environments (Taxi-v3 is one of them), and their environments are a popular way to practice Reinforcement Learning and evaluate Reinforcement Learning algorithms. Feel free to check out their docs to know more about them!

Exploring the environment

It's time we start diving into some code and explore the specifics of the environment we'll be using for Reinforcement learning in this tutorial.

# Let's first install the custom gym module, which contains the environment 
pip uninstall gym -y
pip install git+git://github.com/satwikkansal/gym-dual-taxi.git#"egg=gym&subdirectory=gym/"

import gym
env = gym.make('DualTaxi-v1')
env.render()
# PS: If you're using jupyter notebook and get env not registered error, you have to restart your kernel after installing the custom gym package in the last step.

In the snippet above, we initialized our custom DualTaxi-v1 environment and rendered its current state. In the rendered output,

• The yellow and red rectangles represent both taxis on the 4x4 grid
• R, G, B, and Y are the four possible pick up or drop-off locations for the passenger
• The character "|" represents a wall that the taxis can't cross
• The blue coloured letter represents the pickup location of the passenger
• The purple letter represents the drop-off location.
• Any taxi that gets the passenger aboard would turn green in colour

>>> env.observation_space, env.action_space

(Discrete(6144), Discrete(36))

You might have noticed that the only printed information is their discrete nature and the size of the space. The rest of the details are abstracted. This is an important point, and as you'll realize by the end of the post, our RL algorithm won't need any more information.

However, if you're still curious about how the environment functions, please check out the environment's code and follow the comments there. Another thing that you can do is peek into the state-transition table (check the code in the appendix if you're curious how to do it)

The objective

The objective of the environment is to pick up the passenger from the blue location and drop to the violet location as fast as possible. An intelligent agent should be able to do this with consistency. Now let's see what information we have for the environment's state space (a.k.a observation space) and action space. But before we dive into implementing that intelligent agent, let's see how a random agent would perform in this kind of environment,

def play_random(env, num_episodes):
    """
    Function to play the episodes.
    """
    for i in range(num_episodes):
        state = env.reset()
        done = False
        while not done:
            next_action = env.action_space.sample()
            state, reward, done, _ = env.step(next_action)

# Trying the dumb agent
print_frames(play_random(env, num_episodes=2)) # check github for the code for print_frames

You can see the episode number at the top. In our case, an episode is the timeframe between the steps where the taxis make the first move and the step where they drop a passenger at the desired after picking up. When this happens, the episode is over, and we have to reset the environment to start all over again.

You can see different actions at the bottom, and how the state keeps changing and the agent's reward after every action.

As you might have realized, these taxis are taking a while to finish even a single episode. So our random approach is very dumb for sure. Our intelligent agent definitely will have to perform this task better.

Introducing Q-learning

Q-learning is one among several Reinforcement Learning algorithms. The reason we are picking Q-learning is that it is simple to understand. We'll use Q-learning to make our agent somewhat intelligent.

Intuition behind Q-learning

The way Q-learning works is by storing what we call Q-values for every state-action combination. The Q-value represents the "quality" of an action taken from that state. Of course, the initial q-values are just random numbers, but the goal is to update them in the right direction iteratively. After enough iterations, these Q-values can start to converge (i.e. the update size in upcoming iterations gets so tiny that it has a negligible impact). Once that is the case, we can safely say that,

For a given state, the higher the Q-value for the state-action pair, the higher would be the expected long term reward of taking that particular action.

So long story short, the "developing intelligence" part of Q-learning lies in how the Q-values after agent's interaction with the environment, which requires discussion of two key concepts,

1. The bellman equation

Attached below is the Bellman equation in the context of updating Q-values. This is the equation we use to update Q-values after the agent's interaction with the environment.

The Q-value of a state-action pair is the sum of the instant reward and the discounted future reward (of the resulting state). Where,

• s_t represents the state at time t
• a_t represents action taken at time t (the agent was in state s_t at this point in time)
• r_t is the reward received by performing the action a_t in the state s_t.
• s_t+1 is the next state that our agent will transition to after performing the action a_t in the state s_t.

The discount factor γ(gamma) determines how much importance we want to give to future rewards. A high value for the discount factor (close to 1) captures the effective long-term award, whereas a discount factor of 0 makes our agent consider only immediate reward, hence making it greedy.

The $\alpha$ (alpha) is our learning rate. Like in supervised learning settings, alpha here represents the extent to which our Q-values are being updated in every iteration.

2. Epsilon greedy method

While we keep updating Q-values every iteration, there's an important choice the agent has to make while taking action. The choice it faces is whether to "explore" or "exploit"?

So with time, the Q-values get better at representing the quality of a state-action pair. But to reach that goal, the agent has to try different actions (how can it know if a state-action pair is good if it hasn't tried it?). So it becomes critical for the agent to "explore", i.e. take random actions to gather more knowledge about the environment.

But there's a problem if the agent only explores. Exploration can only get the agent so far. Imagine that the environment agent is in is like a maze. Exploration can put the agent on an unknown path and give feedback to make q-values more valuable. But if the agent is only taking random actions at every step, it will have a hard time reaching the end state of the maze. That's why it is also important to "exploit". The agent should also consider using what it has already learned (i.e. the Q-values) to decided what action to take next.

That's all to say, the agent needs to balance exploitation and exploration. There are many ways to do this. One common way to do it with Q-learning is to have a value called "epsilon", which denotes the probability by which the agent will explore. A higher epsilon value results in interactions with more penalties (on average) which is obvious because we explore and make arbitrary decisions. We can add more sophistication to this method, and it's a common practice that people start with a high epsilon value and keep reducing it as time progresses. This is called epsilon decay. The intuition is that as we keep adding more knowledge to Q-values through exploration, the exploitation becomes more trustworthy, which means we can explore at a lower rate.

Note: There's usually some confusion around if epsilon represents the probability of "exploration" or "exploitation". You'll find it used both ways on the internet and other resources. I find the first way more comfortable as it fits the terminology "epsilon decay". If you see it the other way around, don't get confused, the concept is still the same.

Using Q-learning for our environment

Okay, enough background about Q-learning. Now how do we apply it to our DualTaxi-v1 environment? Because we have two taxis in our environment, we can do it in a couple of ways,

1. Cooperative approach

In this approach, we can assume that a single agent with a single Q-table controls both the taxis (think of it as a taxi agency). The overall goal of this agent would be to maximize the reward these taxis receive combined.

2. Competitive approach

In this approach, we can train two agents (one for each taxi). Every agent has its own Q-table and gets its reward. Of course, the next state of the environment still depends on the actions of both the agents. This creates an interesting dynamic where each taxi would be trained to maximize its individual rewards.

Cooperative approach in action

Before we see the code, let us specify the steps we'd have to take,

1. Initialize the Q-table (size of the Q-table is state_space_size x action_space_size) by all zeros.
2. Decide between exploration and exploitation based on the epsilon value.
3. Exploration: For each state, select any one among all possible actions for the current state (S).
4. Exploitation: For all possible actions from the state (S'), select the one with the highest Q-value.
5. Travel to the next state (S') as a result of that action (a).
6. Update Q-table values using the update equation.
7. If the episode is over (i.e. goal state is reached), reset the environment for the next iteration.
8. Keep repeating steps 2 to 7 until we see decent results in the agent's performance.

from collections import Counter, deque
import random 


def bellman_update(q_table, state, action, next_state, reward):
    """
    Function to perform the q-value update as per bellman equation.
    """
    # Get the old q_value
    old_q_value = q_table[state, action]
    # Find the maximum q_value for the actions in next state
    next_max = np.max(q_table[next_state])
    # Calculate the new q_value as per the equation
    new_q_value = (1 - alpha) * old_q_value + alpha * (reward + gamma * next_max)
    # Finally, update the q_value
    q_table[state, action] = new_q_value


def update(q_table, env, state):
    """
    Selects an action according to epsilon greedy method, performs it, and the calls bellman update
    to update the Q-values.
    """
    if random.uniform(0, 1) > epsilon:
        action = env.action_space.sample()
    else:
        action = np.argmax(q_table[state])

    next_state, reward, done, info = env.step(action)
    bellman_update(q_table, state, action, next_state, reward)
    return next_state, reward, done, info


def train_agent(
        q_table, env, num_episodes, log_every=50000, running_metrics_len=50000,
        evaluate_every=1000, evaluate_trials=200):
    """
    This is the training logic. It takes input as a q-table, the environment.
    The training is done for num_episodes episodes. The results are logged periodically.

    We also record some useful metrics like average reward in the last 50k timesteps, the average length of the last 50 episodes and so on. These are helpful to gauge how the algorithm is performing
    over time.

    After every few episodes of training. We run an evaluation routine, where we just "exploit", i.e. rely on the q-table so far and see how well the agent has learned so far. Over time, the results should get
    better until the q-table starts converging, after which there's negligible change in the results.
    """
    rewards = deque(maxlen=running_metrics_len)
    episode_lengths = deque(maxlen=50)
    total_timesteps = 0

    metrics = {}

    for i in range(num_episodes):
        epochs = 0
        state = env.reset()
        num_penalties, reward= 0, 0
        done = False

        while not done:
            state, reward, done, info = update(q_table, env, state)
            rewards.append(reward)
            epochs += 1
            total_timesteps += 1

            if total_timesteps % log_every == 0:
                rd = Counter(rewards)
                avg_ep_len = np.mean(episode_lengths)
                zeroes, fill_percent = calculate_q_table_metrics(q_table)
                print(f'Current Episode: {i}')
                print(f'Reward distribution: {rd}')
                print(f'Last 10 episode lengths (avg: {avg_ep_len})')
                print(f'{zeroes} Q table zeroes, {fill_percent} percent filled')


        episode_lengths.append(epochs)

        if i % evaluate_every == 0:
            print('===' * 10)
            print(f"Running evaluation after {i} episodes")
            finish_percent, avg_time, penalties = evaluate_agent(q_table, env, evaluate_trials)
            print('===' * 10)
            rd = Counter(rewards)
            avg_ep_len = float(np.mean(episode_lengths))
            zeroes, fill_percent = calculate_q_table_metrics(q_table)

            metrics[i] = {
                    'train_reward_distribution': rd,
                    'train_ep_len': avg_ep_len,
                    'fill_percent': fill_percent,
                    'test_finish_percent': finish_percent,
                    'test_ep_len': avg_time,
                    'test_penalties': penalties
            }

    print("Training finished.")
    return q_table, metrics

def calculate_q_table_metrics(grid):
    """
    This function counts what percentage of cells in the q-table is non-zero.
    Note: Certain state-action combinations are illegal, so the table might never be full.
    """
    r, c = grid.shape
    total = r * c
    count = 0
    for row in grid:
        for cell in row:
            if cell == 0:
                count += 1
    fill_percent = (total - count) / total * 100.0
    return count, fill_percent

def evaluate_agent(q_table, env, num_trials):
    """
    The routine to evaluate an agent. It simply exploits the q-table and records the performance metrics.
    """
    total_epochs, total_penalties, total_wins = 0, 0, 0
    for _ in range(num_trials):
        state = env.reset()
        epochs, num_penalties, wins = 0, 0, 0
        done = False
        while not done:
            next_action = np.argmax(q_table[state])
            state, reward, done, _ = env.step(next_action)
            if reward < -2:
                num_penalties += 1
            elif reward > 10:
                wins += 1
            epochs += 1
        total_epochs += epochs
        total_penalties += num_penalties
        total_wins += wins

    average_penalties, average_time, complete_percent = compute_evaluation_metrics(num_trials,total_epochs,total_penalties,total_wins)
    print_evaluation_metrics(average_penalties,average_time,num_trials,total_wins)
    return complete_percent, average_time, average_penalties

def print_evaluation_metrics(average_penalties, average_time, num_trials, total_wins):
    print("Evaluation results after {} trials".format(num_trials))
    print("Average time steps taken: {}".format(average_time))
    print("Average number of penalties incurred: {}".format(average_penalties))
    print(f"Had {total_wins} wins in {num_trials} episodes")

def compute_evaluation_metrics(num_trials, total_epochs, total_penalties, total_wins):
    average_time = total_epochs / float(num_trials)
    average_penalties = total_penalties / float(num_trials)
    complete_percent = total_wins / num_trials * 100.0
    return average_penalties, average_time, complete_percent

import numpy as np

# The hyper-parameters of Q-learning
alpha = 0.1 # learning rate
gamma = 0.7 # discout factor
epsilon = 0.2
env = gym.make('DualTaxi-v1')
num_episodes = 50000

# Initialize a q-table full of zeroes
q_table = np.zeros([env.observation_space.n, env.action_space.n])
q_table, metrics = train_agent(q_table, env, num_episodes) # Get back trained q-table and metrics

Total encoded states are 6144
==============================
Running evaluation after 0 episodes
Evaluation results after 200 trials
Average time steps taken: 1500.0
Average number of penalties incurred: 1500.0
Had 0 wins in 200 episodes
==============================

----------------------------
Skipping intermediate output
----------------------------


==============================
Running evaluation after 49000 episodes
Evaluation results after 200 trials
Average time steps taken: 210.315
Average number of penalties incurred: 208.585
Had 173 wins in 200 episodes
==============================
Current Episode: 49404
Reward distribution: Counter({-3: 15343, -12: 12055, -4: 11018, -11: 4143, -20: 3906, -30: 1266, -2: 1260, 99: 699, -10: 185, 90: 125})
Last 10 episode lengths (avg: 63.0)
48388 Q table zeroes, 78.12319155092592 percent filled
Training finished.

I have skipped the intermediate output on purpose; you can check this pastebin if you're interested in the entire output.

Competitive Approach

The steps for this are similar to the cooperative approach, with the difference that now we have multiple Q-tables to update.

1. Initialize the Q-table 1 and 2 for both the agents by all zeros. The size of each Q-table is state_space_size x sqrt(action_space_size).
2. Decide between exploration and exploitation based on the epsilon value.
3. Exploration: For each state, select any one among all possible actions for the current state (S).
4. Exploitation: For all possible actions from the state (S'), select the one with the highest Q-value in the Q-tables of respective agents.
5. Transition to the next state (S') as a result of that combined action (a1, a2).
6. Update Q-table values for both the agents using the update equation and respective rewards & actions.
7. If the episode is over (i.e. goal state is reached), reset the environment for the next iteration.
8. Keep repeating steps 2 to 7 until we start seeing decent results in the performance.

def update_multi_agent(q_table1, q_table2, env, state):
    """
    Same as the update method discussed in the last section, just modified for two independent q-tables.
    """
    if random.uniform(0, 1) > epsilon:
        action = env.action_space.sample()
        action1, action2 = env.decode_action(action)
    else:
        action1 = np.argmax(q_table1[state])
        action2 = np.argmax(q_table2[state])
        action = env.encode_action(action1, action2)

    next_state, reward, done, info = env.step(action)
    reward1, reward2 = reward
    bellman_update(q_table1, state, action1, next_state, reward1)
    bellman_update(q_table2, state, action1, next_state, reward2)
    return next_state, reward, done, info


def train_multi_agent(
        q_table1, q_table2, env, num_episodes, log_every=50000, running_metrics_len=50000,
        evaluate_every=1000, evaluate_trials=200):
    """
    Same as the train method discussed in the last section, just modified for two independent q-tables.
    """
    rewards = deque(maxlen=running_metrics_len)
    episode_lengths = deque(maxlen=50)
    total_timesteps = 0

    metrics = {}

    for i in range(num_episodes):
        epochs = 0
        state = env.reset()
        done = False

        while not done:
            # Modification here
            state, reward, done, info = update_multi_agent(q_table1, q_table2, env, state)
            rewards.append(sum(reward))
            epochs += 1
            total_timesteps += 1

            if total_timesteps % log_every == 0:
                rd = Counter(rewards)
                avg_ep_len = np.mean(episode_lengths)
                zeroes1, fill_percent1 = calculate_q_table_metrics(q_table1)
                zeroes2, fill_percent2 = calculate_q_table_metrics(q_table2)
                print(f'Current Episode: {i}')
                print(f'Reward distribution: {rd}')
                print(f'Last 10 episode lengths (avg: {avg_ep_len})')
                print(f'{zeroes1} Q table 1 zeroes, {fill_percent1} percent filled')
                print(f'{zeroes2} Q table 2 zeroes, {fill_percent2} percent filled')


        episode_lengths.append(epochs)

        if i % evaluate_every == 0:
            print('===' * 10)
            print(f"Running evaluation after {i} episodes")
            finish_percent, avg_time, penalties = evaluate_multi_agent(q_table1, q_table2, env, evaluate_trials)
            print('===' * 10)
            rd = Counter(rewards)
            avg_ep_len = float(np.mean(episode_lengths))
            zeroes1, fill_percent1 = calculate_q_table_metrics(q_table1)
            zeroes2, fill_percent2 = calculate_q_table_metrics(q_table2)

            metrics[i] = {
                    'train_reward_distribution': rd,
                    'train_ep_len': avg_ep_len,
                    'fill_percent1': fill_percent1,
                    'fill_percent2': fill_percent2,
                    'test_finish_percent': finish_percent,
                    'test_ep_len': avg_time,
                    'test_penalties': penalties
            }

    print("Training finished.\n")
    return q_table1, q_table2, metrics


def evaluate_multi_agent(q_table1, q_table2, env, num_trials):
    """
    Same as evaluate method discussed in the last section, just modified for two independent q-tables.
    """
    total_epochs, total_penalties, total_wins = 0, 0, 0

    for _ in range(num_trials):
        state = env.reset()
        epochs, num_penalties, wins = 0, 0, 0
        done = False
        while not done:
            # Modification here
            next_action = env.encode_action(
                np.argmax(q_table1[state]),
                np.argmax(q_table2[state]))

            state, reward, done, _ = env.step(next_action)

            reward = sum(reward)

            if reward < -2:
                num_penalties += 1
            elif reward > 10:
                wins += 1

            epochs += 1
        total_epochs += epochs
        total_penalties += num_penalties
        total_wins += wins

    average_penalties, average_time, complete_percent = compute_evaluation_metrics(num_trials,total_epochs,total_penalties,total_wins)
    print_evaluation_metrics(average_penalties,average_time,num_trials,total_wins)
    return complete_percent, average_time, average_penalties

# The hyperparameter of Q-learning
alpha = 0.1
gamma = 0.8
epsilon = 0.2

env_c = gym.make('DualTaxi-v1', competitive=True)

num_episodes = 50000
q_table1 = np.zeros([env_c.observation_space.n, int(np.sqrt(env_c.action_space.n))])
q_table2 = np.zeros([env_c.observation_space.n, int(np.sqrt(env_c.action_space.n))])
q_table1, q_table2, metrics_c = train_multi_agent(q_table1, q_table2, env_c, num_episodes)

Total encoded states are 6144
==============================
Running evaluation after 0 episodes
Evaluation results after 200 trials
Average time steps taken: 1500.0
Average number of penalties incurred: 1500.0
Had 0 wins in 200 episodes
==============================

----------------------------
Skipping intermediate output
----------------------------


==============================
Running evaluation after 48000 episodes
Evaluation results after 200 trials
Average time steps taken: 323.39
Average number of penalties incurred: 322.44
Had 158 wins in 200 episodes
==============================
Current Episode: 48445
Reward distribution: Counter({-12: 13993, -3: 12754, -4: 11561, -20: 3995, -11: 3972, -30: 1907, -10: 649, -2: 524, 90: 476, 99: 169})
Last 10 episode lengths (avg: 78.08)
8064 Q table 1 zeroes, 78.125 percent filled
8064 Q table 2 zeroes, 78.125 percent filled
==============================
Running evaluation after 49000 episodes
Evaluation results after 200 trials
Average time steps taken: 434.975
Average number of penalties incurred: 434.115
Had 143 wins in 200 episodes
==============================
Current Episode: 49063
Reward distribution: Counter({-3: 13928, -12: 13605, -4: 10286, -11: 4542, -20: 3917, -30: 1874, -10: 665, -2: 575, 90: 433, 99: 175})
Last 10 episode lengths (avg: 75.1)
8064 Q table 1 zeroes, 78.125 percent filled
8064 Q table 2 zeroes, 78.125 percent filled
Current Episode: 49706
Reward distribution: Counter({-12: 13870, -3: 13169, -4: 11054, -11: 4251, -20: 3985, -30: 1810, -10: 704, -2: 529, 90: 436, 99: 192})
Last 10 episode lengths (avg: 76.12)
8064 Q table 1 zeroes, 78.125 percent filled
8064 Q table 2 zeroes, 78.125 percent filled
Training finished.

I have skipped the intermediate output on purpose; you can check this pastebin if you're interested in the entire output.

Evaluating the performance

If you observed the code, the train functions returned q-tables as well as some metrics. We can use the q-table now for taking the agent's actions and see how intelligent it has become. Also, we'll try to plot these metrics to visualize how the training progressed.

from collections import defaultdict
import matplotlib.pyplot as plt  
# import seaborn as plt

def plot_metrics(m):
    """
    Plotting various metrics over the number of episodes.
    """
    ep_nums = list(m.keys())
    series = defaultdict(list)
    for ep_num, metrics in m.items():
        for metric_name, metric_val in metrics.items():
            t = type(metric_val)
            if t in [float, int, np.float64]:
                series[metric_name].append(metric_val)

    for m_name, values in series.items():
        plt.plot(ep_nums, values)
        plt.title(m_name)
        plt.xlabel('Number of episodes')
        plt.show()

def play(q_table, env, num_episodes):
    for i in range(num_episodes):
        state = env.reset()
        done = False
        while not done:
            next_action = np.argmax(q_table[state])
            state, reward, done, _ = env.step(next_action)


def play_multi(q_table1, q_table2, env, num_episodes):
    """
    Capture frames by playing using the two q-tables.
    """
    for i in range(num_episodes):
        state = env.reset()
        done = False
        while not done:
            next_action = env.encode_action(
                np.argmax(q_table1[state]),
                np.argmax(q_table2[state]))
            state, reward, done, _ = env.step(next_action)

plot_metrics(metrics)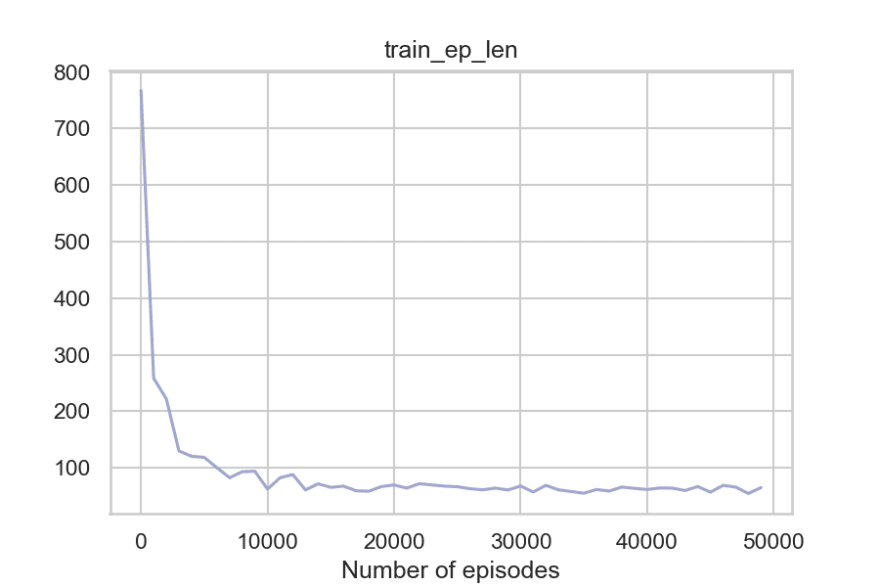

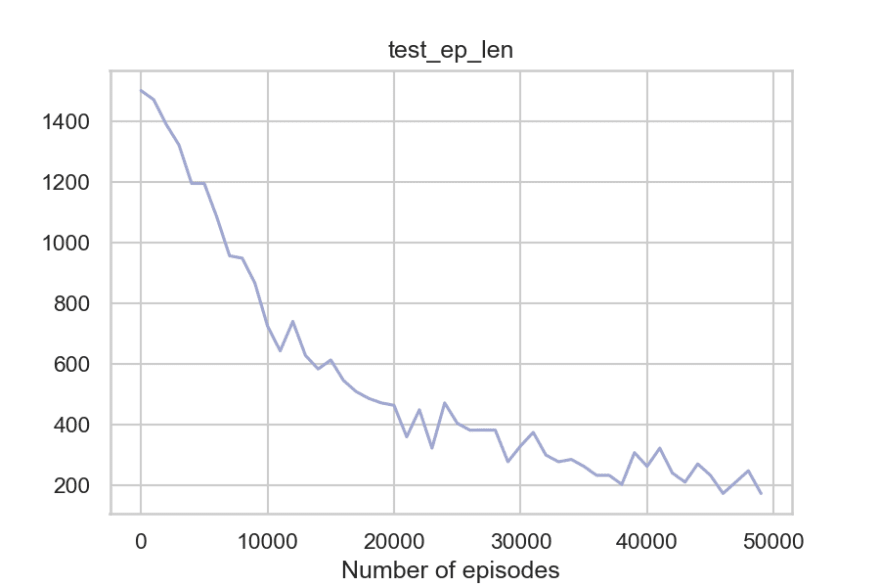
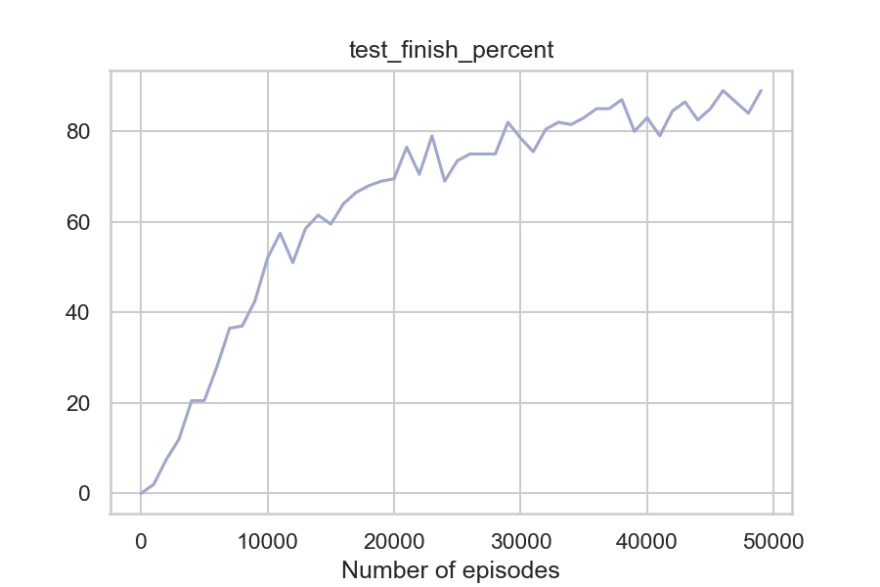
frames = play(q_table, env, 10)
print_frames(frames)

plot_metrics(metrics_c)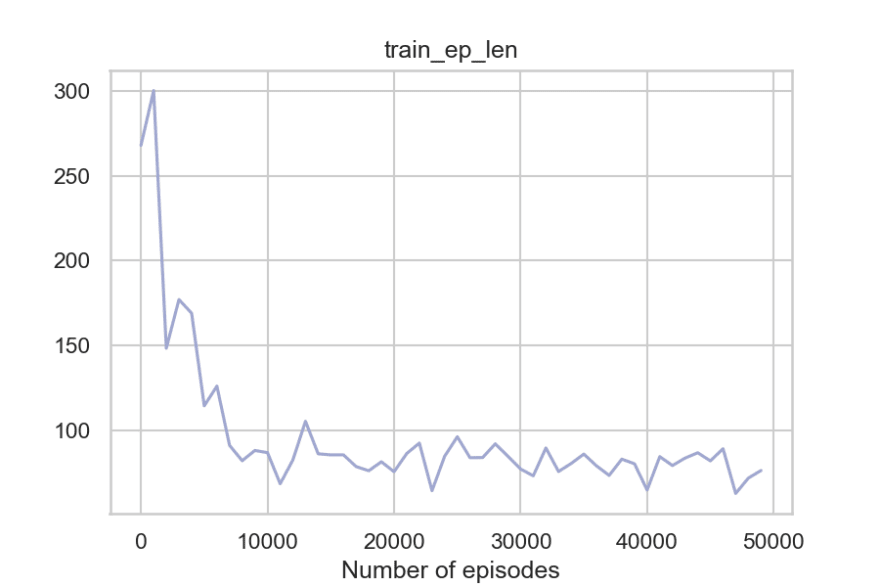

print_frames(play_multi(q_table1, q_table2, env_c, 10))

Some observations

• While Q-learning agent commits errors initially during exploration but once it has explored enough (seen most of the states), it starts to act wisely.
• Both the approaches did reasonably well. However, in relative comparison, the cooperative approach seems to perform better. The plots of the competitive approach are more volatile.
• It took around 2000 episodes for agents to explore most of the possible state-action pairs. Note that not state-action pairs are feasible because some states aren't legal (for example, states where both the taxis are at the exact location, aren't possible).
• As the training progressed, the number of penalties reduced. They didn't reduce entirely because of the epsilon (we're still exploring based on the epsilon value during training).
• The episode length kept decreasing, which means the taxis could pick up and drop the passenger faster because of the newly learned knowledge in q-tables.

So to summarize, the agent can get around the walls, pick the passengers, take fewer penalties, and reach the destination timely. And the fact that the code where q-learning update happens is merely around 20-30 lines of Python code makes it even more impressive.

From what we've discussed so far in the post, you likely have a fair bit of intuition about how Reinforcement Learning works. Now in the last few sections, we will dip our toes in some broader level ideas and concepts that might be relevant to you when exploring Reinforcement Learning further. Let's start with the common challenges of Reinforcement Learning first,

Common challenges while applying Reinforcement learning

Finding the right Hyperparameters

You might be wondering how did I decide on values of alpha, gamma, and epsilon. In the above program, it was mainly based on intuition from my experience and some "hit and trial". This goes a long way, but there are also some techniques to come up with good values. The process in itself is sometimes referred to as Hyperparameter tuning or Hyperparameter optimization.

Tuning the hyperparameters

A simple way to programmatically come up with the best set of hyperparameter values is to create a comprehensive search function that selects the parameters that would result in the best agent performance. A more sophisticated way to get the right combination of hyperparameter values would be to use Genetic Algorithms. Also, it is a common practice to make these parameters dynamic instead of fixed values. For example, in our case, all three hyperparameters can be configured to decrease over time because as the agent continues to learn, it builds up more resilient priors.

Choosing the right algorithms

Q-learning is just one of the many Reinforcement Learning algorithms out there. There are multiple ways to classify Reinforcement Learning algorithms. The selection depends on various factors, including the nature of the environment. For example, if the state space of action space is continuous instead of discrete (imagine that the environment now expects continuous degree values instead of discrete north/east / etc. directions as actions, and the state space consists of more precise lat/long location of taxis instead of grid coordinates), tabular Q-learning can't work. There are hacks to get around continuous spaces (like bucketing their range and making it discrete as a result), but these hacks fail if the state space and action space get too large. In those cases, it is preferred to use more generic algorithms, usually the ones that involve approximators like Neural Networks.

More often than not, in practice, the agent is trained with multiple algorithms initially to decide which algorithm would fit the best.

Reward Structure

It is crucial to think strategically about the rewards to be given to the agent. If the rewards are too sparse, the agent might have difficulty in learning. Poorly structured rewards can also lead to cases of non-convergence and situations in which agent gets stuck in local minima. For example, let's say the environment gave +1 reward for successfully picking up a passenger and no penalty for dropping the passenger. So the agent might end up repeatedly picking up and dropping a passenger to maximize its rewards. Similarly, if there were a very high negative reward for picking up passengers, the agent would eventually learn not to pick a passenger at all, and hence would never finish successfully.

The challenges of real-world environments

Training an agent in an openAI gym environment is relatively easy because you get many things out of the box. The real world, however, is a bit more unorganized. We use sensors to ingest environmental information and translate it into something that can be fed to a Machine Learning algorithm. So such systems involve a lot of techniques overall aside from the learning algorithm. As a simple example, consider a general Reinforcement Learning agent trained to play ATARI games. The information this agent needs to be passed is pixels on the screen. So we might have to use deep learning techniques (like Convolutional Neural Networks) to interpret the pixels on the screen and extract information out of the game (like scores) to enable the agent to interpret the game.

There's also a challenge of sample efficiency. Since the state spaces and action spaces might be continuous and have big ranges, it becomes critical to achieve a decent sample efficiency that makes Reinforcement Learning feasible. If the algorithm needs a high number of episodes (high enough that we cannot make it to produce results in a reasonable amount of time), then Reinforcement Learning becomes impractical.

Respecting the theoretical boundaries

It is easy sometimes to get carried away and see Reinforcement Learning to be the solution to most problems. It helps to have a theoretical understanding of how these algorithm works and fundamental concepts like Markov Decision Processes and awareness of the state of the art algorithms to have a better intuition about what can and what can't be solved using present-day Reinforcement Learning algorithms.

Wrapping up

In this tutorial, we began with understanding Reinforcement Learning with the help of real-world analogies. Then we learned about some fundamental concepts like state, action, and rewards. Next, we went over the process of framing a problem such that we can train an agent through Reinforcement Learning algorithms to solve it.

We took a Self-driving taxi as our reference problem for the rest of the tutorial. We then used OpenAL's gym module in Python to provide us with a related environment to develop our agent and evaluate it. Then we observed how terrible our agent was without using any algorithm to play the game, so we went ahead to implement the Q-learning algorithm from scratch.

We then introduced Q-learning and went over the steps to use it for our environment. We came up with two approaches (cooperative and competitive). We then evaluated the Q-learning results and saw how the agent's performance improved significantly after Q-learning.

As mentioned in the beginning, Reinforcement learning is not just limited to openAI gym environments and games. It is also used for managing portfolio and finances, for making humanoid robots, for manufacturing and inventory management, to develop general AI agents (agents that can perform multiple things with a single algorithm, like the same agent playing multiple Atari games).

Appendix

Further reading

• "Reinforcement Learning: An Introduction" Book by Andrew Barto and Richard S. Sutton. Most popular book about Reinforcement Learning out there. Highly recommended if you're planning to dive deep into the field.
• Lectures by David Silver (also available on YouTube). Another great resource if you're more into learning from videos than books.
• Tutorial series on medium on Reinforcement learning using Tensorflow by Arthur Juliani.
• Some interesting topics related to Multi-Agent environments,
  • Friend and foe Q-learning in general-sum games
  • Game theory concepts like
  • Strictly dominant strategies
  • Nash equilibrium
  • Shapely values for reward distribution

Visualizing the transition table of our dual taxi environment

The following is an attempt to visualize the internal transition table of our environment in a human-readable way. The source of this information is the env.P object which contains a mapping of the form

current_state : action_taken: [(transition_prob, next_state, reward, done)], this is all the info we need to simulate the environment, and this is what we can use to create the transition table.

env.P # First, let's take a peek at this object

{0: {
    0: [(1.0, 0, -30, False)],
  1: [(1.0, 1536, -0.5, True)],
  2: [(1.0, 1560, -0.5, True)],
  3: [(1.0, 1536, -0.5, True)],
  4: [(1.0, 1536, -0.5, True)],
  5: [(1.0, 1536, -0.5, True)],
  6: [(1.0, 96, -0.5, True)],
  7: [(1.0, 0, -30, False)],
  8: [(1.0, 24, -0.5, True)],
  9: [(1.0, 0, -30, False)],
  10: [(1.0, 0, -30, False)],
  11: [(1.0, 0, -30, False)],
  12: [(1.0, 480, -0.5, True)],
  13: [(1.0, 384, -0.5, True)],
  14: [(1.0, 0, -30, False)],
  15: [(1.0, 384, -0.5, True)],
  16: [(1.0, 384, -0.5, True)],
  17: [(1.0, 384, -0.5, True)],
  18: [(1.0, 96, -0.5, True)],
  19: [(1.0, 0, -30, False)],
  20: [(1.0, 24, -0.5, True)],
  21: [(1.0, 0, -30, False)],
  22: [(1.0, 0, -30, False)],
  23: [(1.0, 0, -30, False)],
  24: [(1.0, 96, -0.5, True)],
  25: [(1.0, 0, -30, False)],
  26: [(1.0, 24, -0.5, True)],
  27: [(1.0, 0, -30, False)],
  28: [(1.0, 0, -30, False)],
  29: [(1.0, 0, -30, False)],
  30: [(1.0, 96, -0.5, True)],
  31: [(1.0, 0, -30, False)],
  32: [(1.0, 24, -0.5, True)],
  33: [(1.0, 0, -30, False)],
  34: [(1.0, 0, -30, False)],
  35: [(1.0, 0, -30, False)]},
 1: {0: [(1.0, 1, -30, False)],
  1: [(1.0, 1537, -0.5, True)],
  2: [(1.0, 1561, -0.5, True)],
  3: [(1.0, 1537, -0.5, True)],
  4: [(1.0, 1537, -0.5, True)],
  5: [(1.0, 1537, -0.5, True)],
  6: [(1.0, 97, -0.5, True)],
  7: [(1.0, 1, -30, False)],
  8: [(1.0, 25, -0.5, True)],
  9: [(1.0, 1, -30, False)],
  10: [(1.0, 1, -30, False)],
  11: [(1.0, 1, -30, False)],
  12: [(1.0, 481, -0.5, True)],
  13: [(1.0, 385, -0.5, True)],
  14: [(1.0, 1, -30, False)],
  15: [(1.0, 385, -0.5, True)],
  16: [(1.0, 385, -0.5, True)],
  17: [(1.0, 385, -0.5, True)],
  18: [(1.0, 97, -0.5, True)],
  19: [(1.0, 1, -30, False)],
  20: [(1.0, 25, -0.5, True)],
  21: [(1.0, 1, -30, False)],
  22: [(1.0, 1, -30, False)],
  23: [(1.0, 1, -30, False)],
  24: [(1.0, 97, -0.5, True)],
  25: [(1.0, 1, -30, False)],
  26: [(1.0, 25, -0.5, True)],
  27: [(1.0, 1, -30, False)],
  28: [(1.0, 1, -30, False)],
  29: [(1.0, 1, -30, False)],
  30: [(1.0, 97, -0.5, True)],
  31: [(1.0, 1, -30, False)],
  32: [(1.0, 25, -0.5, True)],
  33: [(1.0, 1, -30, False)],
  34: [(1.0, 1, -30, False)],
  35: [(1.0, 1, -30, False)]},
# omitting the whole output because it's very long!

Now, let's put some code together to convert this information into a more readable tabular form.

! pip install pandas

import pandas as pd
table = []

env_c = gym.make('DualTaxi-v1', competitive=True)

def state_to_human_readable(s):
    passenger_loc = ['R', 'G', 'B', 'Y', 'T1', 'T2'][s[2]]
    destination = ['R', 'G', 'B', 'Y'][s[3]]
    return f'Taxi 1: {s[0]}, Taxi 2: {s[1]}, Pass: {passenger_loc}, Dest: {destination}'

def action_to_human_readable(a):
    actions = 'NSEWPD'
    return actions[a[0]], actions[a[1]]

for state_num, transition_info in env_c.P.items():
    for action, possible_transitions in transition_info.items():
        transition_prob, next_state, reward, done = possible_transitions[0]
        table.append({
            'State': state_to_human_readable(list(env.decode(state_num))),
            'Action': action_to_human_readable(env.decode_action(action)),
            'Probablity': transition_prob,
            'Next State': state_to_human_readable(list(env.decode(next_state))),
            'Reward': reward,
            'Is over': done,
        })
pd.DataFrame(table)

221184 rows × 6 columns

Bloopers

In retrospect, the hardest part of writing this post was to get the dual-taxi-environment working. There were so many moments like below,

It took many trials and errors (tweaking rewards, updating rules for situations like collision, reducing state space) to get to a stage where the solutions for competitive set-ups were converging. The feeling when the solution converges for the first time is very cool. So if you have some free time, I'd recommend you to hack up an environment yourself (the first time I tried q-learning was with a snake-apple game I developed using pygame) and try to solve it with Reinforcement Learning. Trust me, you'll be humbled and learn lots of interesting things along the way!