Reasons To Use Recursion and How It Works

Hello Engineers

Today, I will talk about recursion in what, why, and how.
What is recursion , why to use it, and how to solve problems with it.
The examples will be in Python since Python is easy to understand and close to the algorithms ..

Shall we start ?

What is recursion?

A more complex definition of recursion is: a technique that solve a problem by solving a smaller problems of the same type . We can simplify the definition by saying that recursion is a function that calls itself directly or indirectly. Don't worry for now, it will be much clearer when we start writing our examples.

Why to use recursion?

I choose this question over "when to use recursion" because many learners who studied recursion wanted to know why to use it since that all the problems we can solve in recursion , we can also solve it in normal iterative loops! So here is my answer:

1- Learning recursion makes you a better programmer:

Learning and practicing recursion helps you improve your problem solving skills, because you will learn how to break down bit problems into smaller ones. Also, you will learn the principle of stack in data structure (A stack is an abstract data type that holds an ordered, linear sequence of items), the principle of LIFO (Last In First Out) and how to make use of the call stack.

2- Using recursion makes the code clearer:

Recursion code is simpler and shorter than an iterative code. The recursion function will be written in less lines of code and will be easier for debugging.

3- Recursion is data structure's best friend:

As I mentioned above, recursive functions use the call stack of the interpreter. So, we can make use of the existing of call stack instead of writing code and creating a stack by ourselves or by using any external libraries. which means we can use recursion whenever we want to use stack. Two good implementation examples for using recursion in data structures are trees and graphs in-depth traversal.

How to write recursive functions?

Before writing a recursive function ,let's talk about a few factors to be determined :

1- Determine the size factor:

The size factor means that your problem should not exceed your static value or your memory allocation for that particular program. In simple language your program should not have large numbers and not too many iterations. Because again, recursion functions use call stack and the call stack has a limit. When the stack becomes full the program will crash and you will have an error.

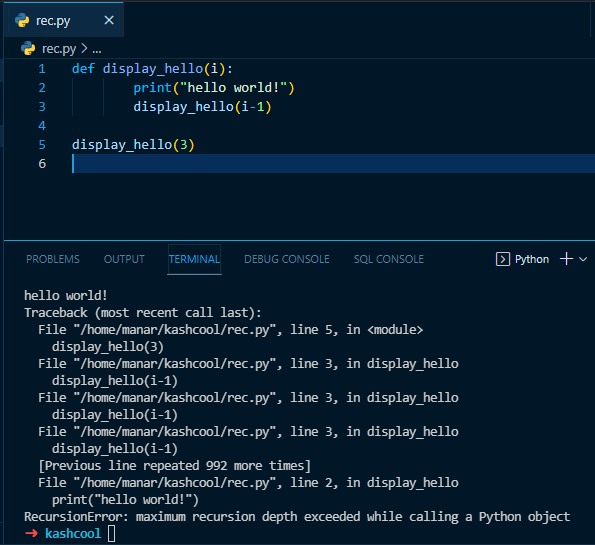
2- Determine the base case/s:

The base cause could be a single or multiple values depending on your program. I will use a while loop here to explain the base case .. if we want to write a program that print "hello world" 5 times using while, we will write:

def display_hello(i):
    while(i > 0):
        print("hello world")
        i -=1

The base cause determines when the loop will stop .. in our example the base cause is i=0 because when the value of i becomes zero the loop will break and stop.

Base case in recursion is that particular value that if we reach we want to stop recalling of the function and start removing and executing every function in the call stack.

Not having a base cause will make the function call itself until the call stack becomes full and the program crashes. Also, having a wrong base cause will result to a wrong output.

3- Determine the general case/s:
General cause is the one where the problem expressed as a small version of itself. Which means, the program will continue iterate the general causes until it reaches the base cause

In our example above, when i=0 considered as the base cause and we send 5 as a parameter , then we can think of:
i=1, i=2, i=3, i=4, and i=5 as the general causes.

Now, let's Write a recursive function and trace it using the previous problem:

We want to write a function that write "hello world" 3 times:

Let's analyze the problem:

The function will check the base cause, if the current case doesn't match the base cause then the function will call itself one time .. So the increasing is a liner (it could be O(n)) (it will be probably safe for the call stack size)
let's try writing our function now by using our while loop example

1- The base cause -> i =0

def display_hello(i):
   if i>0:

2- The print command -> print("hello world")

def display_hello(i):
   if i>0:
       print("hello world")

3- The changes in every iteration -> i-=1
to send the new value of the variable to the next function call we have to write it as a parameter

def display_hello(i):
   if i>0:
       print("hello world")
       display_hello(i-1)

And that's it for this small problem .. Before tracing it let's add one print command after the function call and show the result at the end to make the tracing more interesting

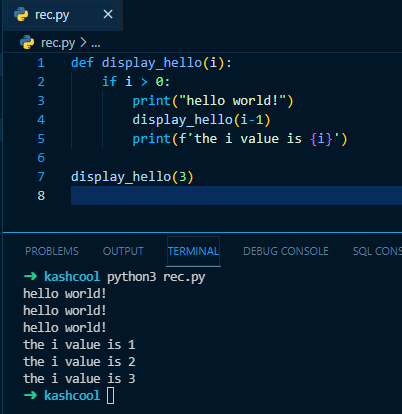
Assuming that the first invocation was :

display_hello(3)

And our function is :

def display_hello(i):
    if i > 0:
        print("hello world!")
        display_hello(i-1)
        print(f'The i value is {i}')

Now we will trace it.

In the first call the function will enter the call stack

Then the program will execute the commands :

When the execution reaches line 4 (the function recall) it will stop there (it will pause the execution of the rest commands) and add another function to the stack :

Then the program will execute the commands in the second recalled function :

Again , when the execution reaches line 4 (the function recall) it will stop there (it will pause the execution of the rest commands) and add another function to the stack :

For this time too , our base cause has not satisfied yet because i is still bigger than zero, so the execution will continue until the function recall and then adds another function to the stack.

Now finally the parameter is 0 which is the value of i

The execution will start until line 2 because the condition says that i should be bigger than zero, but i is equal to zero .. So we reached the base cause and we will not reach the recall "invocation" and the prints

Because this function finished all the commands that should be executed, it's the time to pop the function out of the stack :

Now we returned to the previous function when the parameter was 1
so now the program will execute the rest of the command/s:

The function now is completed all the commands that should be executed, time to pop the function out of the stack :

Now we returned to the function that its parameter is two and we will execute the rest of the commands :

Again, after we done the execution we will remove the function from the stack:

Now we have the first call which 3 was its parameter, and we will execute the rest of the commands:

And here the last function will pop out from the stack and the call stack will become empty and here is the end of our program:

Let's check if our tracing was right by executing the code :

So here we reach the end of today's article

Happy recursion 😁

Author Note:

I didn't use Fibonacci as an example because I believe that it is not a good example for teaching recursion and recursion is one of the worst solutions to solve Fibonacci in terms of both time and space.
View this article Fibonacci without recursiveness in Python - a better way