36
The (not) Legitimate Case Against Bayes
Imagine a world where Reverend Thomas Bayes never had his work published, it would be a pure sanctuary. Remember in Star Wars: The Empire Strikes Back when Han Solo was trying to navigate through an asteroid belt and C3P0 tried to warn him that the odds were "very low". Han Solo, being the badass he was, responded "Never tell me the odds!" in my dream world, without Bayes, we literally couldn't tell him!


Ok.. that's not how it actually works, but in my mind, the confusing logic of Bayes has turned him into a bit of a villain in my world. Trying to put his logic into python, to me, is like trying to get oil and water to mix.
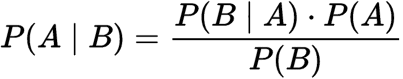
P() = "Probability of"
A = "Event A"
B = "Event B"
| = "Given that"
A = "Event A"
B = "Event B"
| = "Given that"
So if we write this out in English.
The probability of event A given event B occurs equals the probability of event B given event A multiplied by the probability of event A divided by the probability of event B
OK, easy right? totally makes sense and isn't gonna be confusing when we put it in a real-world example right?
(the exact numbers of the example come from a video by 3Blue1Brown on YouTube)
Let's say that we sampled 1000 women and found out that 1% of them had breast cancer. If we tested them, what are the odds of having breast cancer after testing positive? When I first went through the problem I optimistically replied "it says one percent?" WRONG. Bayes theory is as much about logic as it is 'math' (If anyone here says anything about math being logical they can refer themselves to this chart I made them). We have to also understand the validity of the test.
Of the ten people who actually have breast cancer, 9 receive true positives and one receives a false negative on their breast cancer screening.
Of the other 990 women, 89 receive false positives, and the remaining 901 receive true negatives.
Now we have enough information to take steps in answering the question "what are the odds of having breast cancer after testing positive?"
We have to be careful when trying to answer this. We need to identify how accurate the test is when the women do have breast cancer vs when they don't. We can start with a true positive rate of 90% (only one false negative) and then the odds you test negative when you don't have the disease, which is about 91% (901 true negatives over 990 non-diseased)
To recap, we know that 1% of women have cancer (10 people)
90% of people with the disease get a positive result (9 people)
91% of people without the disease get a true negative (901 people)
90% of people with the disease get a positive result (9 people)
91% of people without the disease get a true negative (901 people)
All we have to do is apply Bayes theorem to find out how many women have the disease after testing positive.
P(A) = (.01)
P(B) = (.91)
P(B|A) = (.9)
P(B) = (.91)
P(B|A) = (.9)
P(A|B) = (.9 + .01) * (.01)
_________________
(.91)
_________________
(.91)
We find that the probability of having breast cancer after testing positive is about 1/11
This makes my original 'guess' of 90% accuracy kind of uhhh seem not smart we'll say. It also shows that we need logic for real-life situations that apply probability to those issues, such as, medical tests.
Suppressing the urge to make about 4 sarcastic comments, we use Bayes Theorem if we have a hypothesis, we have some observed evidence, and we want the probability of the Hypothesis, given the evidence. This thought is expressed more clearly in this video at around the 5 minute mark. After we formulate a hypothesis, we want to see if it stands up to the observed/new data, Bayes Theorem provides a way to clearly show statistical proof on the probability of your hypothesis (validates or invalidates your model).
As an aspiring Data Scientist, one way we use Bayes Theorem is when we build AI and want to "explicitly and numerically model a machine's belief."
Essentially, when you are feeling extra sadistic and want others to struggle as they read through your proof on probabilities of certain events, is a perfect time to use Bayes Theorem.
Bayes had the common sense NOT to publish his findings, he knew that they were too powerful, or too confusing? I'm really not sure which at this point but he didn't think it was worth the publish. So the man EQUALLY guilty for all my recent struggles is named Richard Price.
After Bayes passed away he found the theorem in his papers and decided to publish it for him posthumously, in most cases that would be an honorable thing to do, in Price's case it has set things into motion that will make a random 21-year-old complain about probability to anybody in earshot of him.
I now wake up with the mentality of "What is the probability that I annoy someone with Bayes slander GIVEN THAT ... I wake up.." I have found the answer to be very high/likely.
So many people wake up and just accept that certain things are "necessary evils". How many times have we heard "Mondays am I right?" or literally anything about the DMV. Maybe Bayes Theorem clicks in other people's minds, but in mine, it's as clear as the Electoral College. I look forward to the day where me and the ghost of Reverend Thomas Bayes can kick back and laugh at my inability to apply his principles to my models and/or basic logic.
36
