14
Functions: Am I pure?
One might have noticed that functional programmers are the biggest admirers of pure functions -functions with no side effects and believe me functional programming and pure functions have some desirable properties, that are much rather well said than proper implemented. un-fortunately this fascination with pure function, what it stands for and what we can do with it, is somewhere I feel the reason for why Functional Programming is a bit of disconnected from the industry. As we'll soon realize that there is very less "purity" in most of the real-world application.
In this post we'll try to understand what are functions, what purity means to them and how purity affect our programs.
From our beautiful memories of high school algebra or set theory we remember that a mathematical function maps the domain to range. Now, If you are like "My god! now what are these terms, I don't recall learning any such things...", then don't worry we'll quickly try to summarize these below.
TL;DR In programmers analogy a function maps the argument to the return value (also called as main effect).
Functions in mathematics formalized in set theory is a map(binary relation) between two sets respectively called as domain and co-domain/range , which associates each element of first set(input) to exactly one element of second set(output). Can be represented as f: x -> y. Now, if the function is denoted by f then the relation(that associates) is denoted by y = f(x) read as "f of x", where x,y are elements of domain and co-domain respectively. x is also often called as argument/input of the function f and y is the value, the output or the image of f(x).
That's all there is to a function, the mapping could be anything, maybe based on some formula or could be completely arbitrary. A function is completely abstract mathematical object and the value that the function yields is completely determined by its inputs.
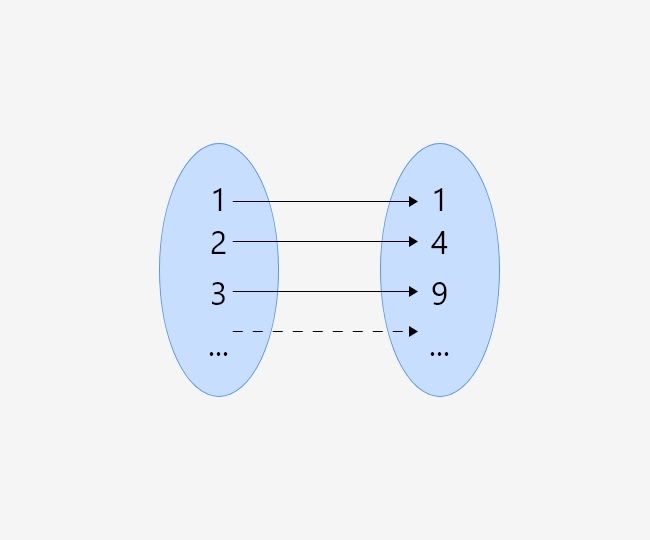
For example consider a function f mapping a set of numbers to their squares, Here in this case the domain set would be {1, 2, 3 ,4,...} and the co-domain would be {1, 4, 9, 16, ...} as shown in the above image, Now how can you represent this mathematical function in terms of programming. Lets try this out below
/*
* domain: number
* co-domain: number
* square: x -> x * x
*/
function square(x: number): number {
return x * x;
}As in the above code square is the function that maps the elements of the domain (inputs/arguments) with the element of the co-domain output. This function as said above completely yields the value based on its inputs and nothing else matters to it.
Mathematical functions exist in something like a vacuum meaning that their results are strictly and only depend on their own arguments and nothing else, you'll see that this is not usually the case with functions in programming.
Functional Programming(FP) is a programming style which emphasis on functions, and so its fundamental operation is the application of functions to arguments, The main program is itself a function that receives the programs input as its arguments and program's output as its result. Generally the main function consists of many functions. One of the special characteristics of mainstream functional programming languages are that they functional programs do not have assignment statements, so once a value is assigned can never change, generally speaking they contain no side effects at all.
Even though some of the functions in programming are close representations/resemblances to mathematical functions, they're usually not the case. As we saw above that mathematical functions are completely abstract entities, and in case of programming we usually want a function to manipulate things that are rendered on the screen, interact with some other system or maybe process a file. Another important difference to ponder is that functions have access to all the outer scope and context or even things that are completely outside its own scope and the scope of the program such as a database connection or some remote API service. As these context exist we are able to change things that are outside the control of the program. Meaning the functions in programming are substantially more complex in terms of their behavior, implementations and separation of concerns. These very differences between the two type of functions has led us to distinction between pure and impure functions.
However the term pure functions doesn't come from mathematics and neither by imperative programming languages, but rather came from languages that allowed side-effects(impure functional programming languages).
The very first characteristic that makes a function a Pure function is that its execution cannot depend on any implicit knowledge about the outer world. The only knowledge it has and affects its evaluation is gained and inferred from the input that is passed into it. This is what it means to be isolated. A function is said to be isolated if the only information of the external world that it is aware of is gained or inferred by the inputs passed via arguments to the function.
💡 A pure function is always isolated.
A side-effect is any external effect a function has beside a return value, And usually a function is said to have external effect if it
- modifies/mutates some state variable outside its local scope/environment.
- modifies/mutates mutable input arguments(in case of passed by reference).
- throwing exceptions or performing some kind of I/O operations includes things such as interacting with processes outside the application's boundary, like interacting with database, a filesystem or a console.
💡 A pure function has no side-effects
A function or expression(in case of mathematics) is called as Referentially transparent if it can be replaced with its corresponding value without changing the behavior of the program, means that when a function call can directly replaced by its return value. To do so the function must be pure, the returned value must be same for given input. for example consider an example below
function doubleNum(num:number): number {
return 2 * num;
}
const x = doubleNum(3); //6
// should be same as
const x = 6;
// then doubleNum(num) is said to referentially transparentThe importance of referential transparency is that it allows the compilers in thing like optimizing code, memorization, subexpression elimination, simplifying complexity. Few of the functional programming languages enforce referential transparency whenever possible.
you'll can refer this Stackoverflow answer for a detailed explanation.
💡 A Pure functions is referentially transparent.
Pure functions are the ones that closely resemble mathematical functions abstracted from the outer context they do nothing but compute an output based on their input values. No other factors are allowed have any effects on its functionality, thus no side effects makes them pure. So, In summary a pure functions
- Have no side-effects.
- Output is solely determined upon the provided inputs.
- Given same input will always produce same output(are referentially transparent).
Pure functions are idempotent meaning there are no limits to how many times a pure function may be invoked, and as given above, no matter how may times it is invoked, it always returns the same output for same input.
In functional programming the ideal function is the one that is pure, A pure function always returns the same output for same input and has no side-effects, Since these pure functions are independent of existence of the any external context, Because of these isolation characteristics of pure function they are quite easily testable with unit test.
A unit test is testing a way to test unit -a small piece of code that can be logically separated/isolated.
So as one might have noticed the word isolated in the definition, In order to perform unit test we have to first able to isolate the unit from its dependencies, so that its self-capable of performing the intended operations without any awareness of the external world. This very nature of unit aligns completely with purity of a pure function. Pure functions are also have referential transparency and idempotent nature, which makes it much easier to infer and predict the output for a given input which makes the code greatly testable. So, an ideal functional design is not just ideal, but also perfectly testable.
Pure functions form the foundations of functional programs, and since they're completely unaware of the outer context they are immune to a whole lot of bugs and errors. The deterministic nature(same output for the same input) of such functions make them easy to test. Whether you evaluate the function now or later sometime, the order of invoking a pure function will not change its output result. This makes our code more flexible for re-organizing, refactoring, also further more if our application consists entirely of pure functions then we can take advantage of techniques as lazy evaluation, Parallelization, memorization for performance benefits.
Pure functional code also makes our program maintainable, reusable, composable, memorizable, and suitable candidate for parallelization. For such reasons it is recommended to make use of pure functions whenever possible.
👉 This blogpost was originally publish at my personal blog site
14
